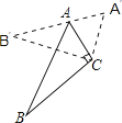
[题目]如图.△ABC中.∠ACB=90°.∠ABC=32°.以点C为旋转中心顺时针旋转后得到△A′B′C.且点A在边A′B′上.则旋转角的度数为．题目和参考答案——青夏教育精英家教网—

【题目】如图，△ABC中，∠ACB=90°，∠ABC=32°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为______．

【答案】64°

【解析】

先利用互余计算出∠BAC=58°，再利用旋转的性质得CA=CA′，∠A′=∠BAC=58°，∠ACA′等于旋转角，根据等腰三角形的性质和三角形内角和计算出∠ACA′的度数即可．

解：∵∠ACB=90°，∠ABC=32°，
∴∠BAC=58°，
∵以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，
∴CA=CA′，∠A′=∠BAC=58°，∠ACA′等于旋转角，
∴∠CAA′=∠A′=58°，
∴∠ACA′=180°-58°-58°=64°，
即旋转角的度数为64°．

故答案为：64°．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】已知函数y=（m﹣2）xm2+m-4 +2x﹣1是一个二次函数，求该二次函数的解析式．

【答案】y=﹣5x2+2x﹣1

【解析】试题分析：根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0，由此求得m的值，进而得到该二次函数的解析式．

试题解析：依题意得：m2+m﹣4=2且m﹣2≠0．即（m﹣2）（m+3）=0且m﹣2≠0，

解得m=﹣3，

则该二次函数的解析式为y=﹣5x2+2x﹣1

【题型】解答题
【结束】
21

【题目】如图，在ABCD中，EF∥AB，FG∥ED，DE：DA=2：5，EF=4，求线段CG的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与X轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：

①4a﹣2b+c＜0；②2a﹣b＜0；③a+c＜1；④b2+8a＞4ac，

其中正确的有（）

A．1个 B．2个 C．3个 D．4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某商店销售一种旅游纪念品，第一周的营业额为200元，第二周该商店对纪念品打8折销售，结果销售量增加3件，营业额增加了40%．

（1）求该商店第二周的营业额；

（2）求第一周该种纪念品每件的销售价格．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为了保护环境，某集团决定购买、两种型号的污水处理设备共10台，其中每台价格及月处理污水量如下表：


价格（万元/元）	15	12
处理污水量（吨/月）	250	220

经预算，该集团准备购买设备的资金不高于130万元.

（1）请你设计该企业有哪几种购买方案？

（2）试通过计算，说明哪种方案处理污水多？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】“蘑菇石”是我国著名的自然保护区梵净山的标志，小明从山脚B点先乘坐缆车到达观景平台DE观景，然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点，“蘑菇石”A点到水平面BC的垂直距离为1890m．如图，DE∥BC，BD=1800m，∠DBC=80°，求斜坡AE的长度．（结果精确到0.1m，可参考数据sin29°≈0.4848，sin80°≈0.9848，cos29°≈0.8746，cos80°≈0.1736）