
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
【答案】D
【解析】
试题分析:①将x=﹣2代入y=ax2+bx+c,可以结合图象得出x=﹣2时,y<0;
②由抛物线开口向下,可得a<0;由图象知抛物线的对称轴大于﹣1,则有x=![]() >﹣1,即可得出2a﹣b<0;
>﹣1,即可得出2a﹣b<0;
③已知抛物线经过(﹣1,2),即a﹣b+c=2(1),由图象知:当x=1时,y<0,即a+b+c<0(2),联立(1)(2),可得a+c<1;
④由抛物线的对称轴大于﹣1,可知抛物线的顶点纵坐标应该大于2,结合顶点的纵坐标与a<0,可以得到b2+8a>4ac.
解:①由函数的图象可得:当x=﹣2时,y<0,即y=4a﹣2b+c<0,故①正确;
②由函数的图象可知:抛物线开口向下,则a<0;抛物线的对称轴大于﹣1,即x=![]() >﹣1,得出2a﹣b<0,故②正确;
>﹣1,得出2a﹣b<0,故②正确;
③已知抛物线经过(﹣1,2),即a﹣b+c=2(1),由图象知:当x=1时,y<0,即a+b+c<0(2),
联立(1)(2),得:a+c<1,故③正确;
④由于抛物线的对称轴大于﹣1,所以抛物线的顶点纵坐标应该大于2,即:![]() >2,由于a<0,所以4ac﹣b2<8a,即b2+8a>4ac,故④正确,
>2,由于a<0,所以4ac﹣b2<8a,即b2+8a>4ac,故④正确,
故选D.


科目:初中数学 来源: 题型:
【题目】计算或化简(整式乘法)
(1). (-3ab)· (- 4b)2 ; (2).![]() .
.
(3). 3x(x2-2x-1)+6x (4).![]() +(-x+1)(x-2)
+(-x+1)(x-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决后面的问题。
材料:我们知道,n个相同的因数a相乘![]() 可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)
可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)
一般地,若an=b (a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4)
(1)计算以下各对数的值:log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
(3)根据(2)的结果,我们可以归纳出:logaM+logaN=logaM N (a>0且a≠1,M>0,N>0),请你根据幂的运算法则:am=an+m以及对数的定义证明该结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;
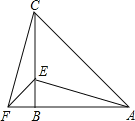
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
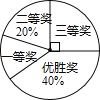
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 填空题:如图,AB//CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数。

解:![]() ,(已知)
,(已知)
![]() ,(等量代换)
,(等量代换)
![]() PN // CD,( )
PN // CD,( )
![]() _________=180°,( )
_________=180°,( )
![]() ,(已知)
,(已知)
![]()
![]() ,(已知)
,(已知)
![]()
![]() ____________,(两直线平行,内错角相等)
____________,(两直线平行,内错角相等)
![]() ,(已知)
,(已知)
![]() __________,(等量代换)
__________,(等量代换)
![]()
![]() BCP=
BCP=![]() BCD-
BCD-![]() PCD=____________°-30°=_________°.
PCD=____________°-30°=_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC, GH∥AC, DI∥AB.

(1)写出与∠IEC是同旁内角的角。
(2)判断∠GHC与∠FEC是否相等,并说明理由。
(3)若EI平分∠FEC,∠C=56°,∠B=50°,求∠EID的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com