
【题目】阅读下列材料,并解决后面的问题。
材料:我们知道,n个相同的因数a相乘![]() 可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)
可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)
一般地,若an=b (a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4)
(1)计算以下各对数的值:log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
(3)根据(2)的结果,我们可以归纳出:logaM+logaN=logaM N (a>0且a≠1,M>0,N>0),请你根据幂的运算法则:am=an+m以及对数的定义证明该结论。
【答案】6;log264;loga(MN);证明见解析.
【解析】试题分析:首先认真阅读题目,准确理解对数的定义,把握好对数与指数的关系.
(1)根据对数的定义求解;
(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;
(3)有特殊到一般,得出结论:logaM+logaN=loga(MN);
(4)首先可设logaM=b1,logaN=b2,再根据幂的运算法则:anam=an+m以及对数的含义证明结论.
试题解析:(1)log24=2,log216=4,log264=6;
(2)4×16=64,log24+log216=log264;
(3)logaM+logaN=loga(MN);
(4)证明:设logaM=b1,logaN=b2,
则ab1=M,ab2=N,
∴MN=ab1ab2=ab1+b2,
∴b1+b2=loga(MN)即logaM+logaN=loga(MN).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 相交于A(﹣1,2),B(2,m)两点,与y轴相交于点C.
相交于A(﹣1,2),B(2,m)两点,与y轴相交于点C.
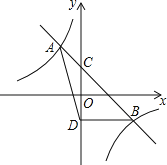
(1)求k1、k2、m的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA, OE平分∠DOC.
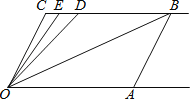
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
A. (-2,-3) B. (-2,3) C. (2,-3) D. (2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=﹣x2+x+2,则当y<0时,自变量x的取值范围是( )
A.x<﹣1或x>2 B.﹣1<x<2
C.x<﹣2或x>1 D.﹣2<x<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.

(1)求过A、B、C三点的抛物线的解析式;
(2)若直线CD∥AB交抛物线于D点,求D点的坐标;
(3)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com