
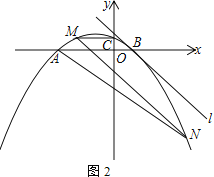
【题目】已知:抛物线y=a(x-m)(x+3m)(a<0,m>0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,直线l:y=kx+b经过点B,且与该抛物线有唯一公共点,平移直线l交抛物线于M、N两点(点M、N分别位于x轴上方和下方)
(1) 若![]() ,C(0,
,C(0,![]() )
)
① 求该抛物线的解析式
② 如图1,连接AM、AN,求证:∠MAB=∠NAB
(2) 如图2,连接MC.若MC∥x轴,求![]() 的值
的值

【答案】(1)①![]() ;② 证明见解析;(2)
;② 证明见解析;(2)![]()
【解析】(1)①利用a的值和点C的坐标,代入求解即可得到函数的解析式;
②过点M作MD⊥x轴于D,过点N作NE⊥x轴于E,由一次函数和二次函数的解析式联立方程组求参数的值,然后得出直线MN,联立方程组求出AD·NE-AE·MD=0,证明△MDA∽△NEA即可得解;
(2)设直线l:y=kx+b,联立方程组,化简后通过一元一次方程的根的判别式和线段的长求出比例即可.
(1) ① 当![]() 时,
时,![]()
将C(0,![]() )代入
)代入![]() 中,得
中,得![]() ,m=±1
,m=±1
∵m>0
∴m=1
∴![]()
② 过点M作MD⊥x轴于D,过点N作NE⊥x轴于E
设直线l:y=kx-k,M(x1,y1)、N(x2,y2)
联立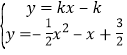 ,整理得
,整理得![]()
∵直线l与抛物线只有一个公共点
∴△=4(k+2)2=0,解得k=-2
设直线MN:y=-2x+t
联立 ,整理得x2-2x+2t-3=0
,整理得x2-2x+2t-3=0
∴x1+x2=2,x1x2=2t-3
∴AD·NE-AE·MD=(x1+3)(-y2)-(x2+3)y1=4x1x2+(6-t)(x1+x2)-6t
=4(2t-3)+(6-t)·2-6t=0
∴AD·NE=AE·MD
即![]()
又∠MDA=∠NEA=90°
∴△MDA∽△NEA
∴∠MAB=∠NAB
(2) y=a(x2+2mx-3m2)=ax2+2amx-3am2
设直线l:y=kx+b
将B(m,0)代入y=kx+b得,km+b=0,b=-km
∴y=kx-km
联立![]() ,整理得ax2+(2am-k)x-3am2+km=0
,整理得ax2+(2am-k)x-3am2+km=0
∴△=(2am-k)2-4a(-3am2+km)=0,得k=4am
∴直线l:y=4amx-4am2
∴M(-2m,-3am2)
∴直线MN的解析式为:y=4amx+5am2
联立![]() ,整理得ax2-2amx-8am2=0
,整理得ax2-2amx-8am2=0
∴xM·xN=-8m2
又xM=-2m
∴xN=4m
∴N(4m,21am2)
∴AM2=m2+9a2m4,AN2=49m2+212a2m4
∴![]() ,
,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
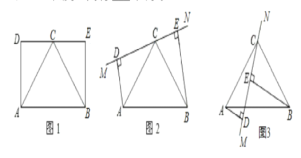
(1)由图1通过观察、猜想可以得到线段AC与线段BC的数量关系为___,位置关系为__;
(2)保持图1中的△ABC固定不变,绕点C旋转DE所在的直线MN到图2中的位置(当垂线AD、BE在直线MN的同侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明(第一问中得到的猜想结论可以直接在证明中使用);
(3)保持图2中的△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有___关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的某圆上,有弦MN,取MN的中点P,我们规定:点P到某点(直线)的距离叫做“弦中距”,用符号“![]() ”表示.
”表示.
现请在以W(-3,0)为圆心,半径为2的⊙W圆上,根据以下条件解答所提问题:
(1)已知弦MN长度为2.
①如图1:当MN∥x轴时,直接写出到原点O的![]() 的长度;
的长度;
②如果MN在圆上运动时,在图2中画出示意图,并直接写出到点O的![]() 的取值范围.
的取值范围.
(2)已知点![]() ,点N为⊙W上的一动点,有直线
,点N为⊙W上的一动点,有直线![]() ,求到直线
,求到直线![]() 的
的![]() 的最大值.
的最大值.
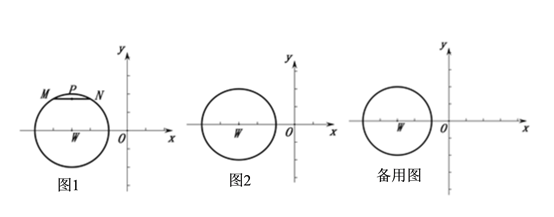
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市晶泰星公司安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品.根据市场行情测得,甲产品每件可获利
件乙产品.根据市场行情测得,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产
元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产![]() 件乙产品,当天每件乙产品平均荻利减少
件乙产品,当天每件乙产品平均荻利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
| ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解该市九年级学生上学期参加综合实践活动的情况,随机调查了该市光明中学九年级学生上学期参加综合实践活动的时间,并用得到的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,回答下列问题:
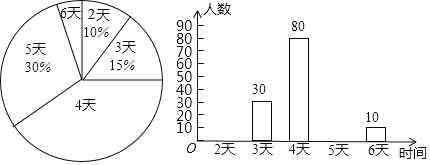
(1)试求出该校九年级学生总数;
(2)分别求出活动时间为2天、5天的学生人数,并补全条形统计图;
(3)如果该市九年级学生共约50000人,请你估计“活动时间不少于4天”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级二班的几位同学正在一起讨论一个关于数轴上的点表示数的题目:
甲说:“这条数轴上的两个点![]() 、
、![]() 表示的数都是绝对值是4的数”;
表示的数都是绝对值是4的数”;
乙说:“点![]() 表示负整数,点
表示负整数,点![]() 表示正整数,且这两个数的差是3”;
表示正整数,且这两个数的差是3”;
丙说:“点![]() 表示的数的相反数是它本身”.
表示的数的相反数是它本身”.
(1)请你根据以上三位同学的发言,画出一条数轴,并描出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个不同的点.
五个不同的点.
(2)求这个五个点表示的数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
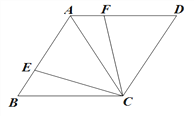
【题目】如图,四边形ABCD中,∠B=60°,对角线AC=BC,点E在AB上,将CE绕点C顺时针旋转60得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com