
分析 分类讨论:①以OM为底时,点M的个数;②以AM为底时,点M的个数;③以AO为底边时,点M的个数.
解答 解:因为△AOM为等腰三角形,所以可分成三类讨论:
①AO=AM(有一个)
此时只要以A为圆心AO长为半径画圆,可知圆与y轴交于O点和另一个点,另一个点就是M;
②AO=OM(有两个)
此时只要以O为圆心AO长为半径画圆,可知圆与y轴交于两个点,这两个点就是M的两种选择(AO=OM=R)
③AM=OM(一个)
作AO的中垂线,与y轴有一个交点,该交点就是点M的最后一种选择.(利用中垂线性质)
综上所述,共有4个.
故答案为:4.
点评 本题考查了等腰三角形的判定及坐标与图形的性质;解答本题极易漏解,所以解答时,应利用“分类讨论”的数学思想.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
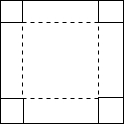 如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3.
如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
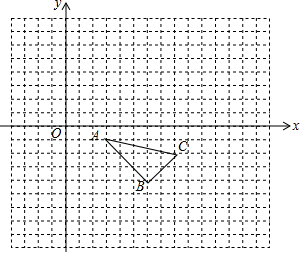 如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
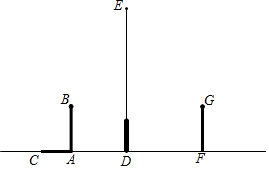 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com