
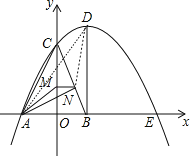
【题目】如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.

【答案】(1)抛物线解析式为y=﹣![]() x2+
x2+![]() x+4;D点坐标为(3,5);(2)M点的坐标为(0,
x+4;D点坐标为(3,5);(2)M点的坐标为(0,![]() )或(0,
)或(0,![]() );(3)AM+AN的最小值为
);(3)AM+AN的最小值为![]() .
.
【解析】(1)利用待定系数法求抛物线解析式;利用等腰三角形的性质得B(3,0),然后计算自变量为3所对应的二次函数值可得到D点坐标;
(2)利用勾股定理计算出BC=5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,由于∠MCN=∠OCB,根据相似三角形的判定方法,当![]() 时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即
时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即![]() ;当
;当![]() 时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即
时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即![]() ,然后分别求出m的值即可得到M点的坐标;
,然后分别求出m的值即可得到M点的坐标;
(3)连接DN,AD,如图,先证明△ACM≌△DBN,则AM=DN,所以AM+AN=DN+AN,利用三角形三边的关系得到DN+AN≥AD(当且仅当点A、N、D共线时取等号),然后计算出AD即可.
(1)把A(﹣3,0),C(0,4)代入y=ax2﹣5ax+c得![]() ,解得
,解得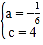 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
∵AC=BC,CO⊥AB,
∴OB=OA=3,
∴B(3,0),
∵BD⊥x轴交抛物线于点D,
∴D点的横坐标为3,
当x=3时,y=﹣![]() ×9+
×9+![]() ×3+4=5,
×3+4=5,
∴D点坐标为(3,5);
(2)在Rt△OBC中,BC=![]() =5,
=5,
设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,
∵∠MCN=∠OCB,
∴当![]() 时,△CMN∽△COB,则∠CMN=∠COB=90°,
时,△CMN∽△COB,则∠CMN=∠COB=90°,
即![]() ,解得m=
,解得m=![]() ,此时M点坐标为(0,
,此时M点坐标为(0,![]() );
);
当![]() 时,△CMN∽△CBO,则∠CNM=∠COB=90°,
时,△CMN∽△CBO,则∠CNM=∠COB=90°,
即![]() ,解得m=
,解得m=![]() ,此时M点坐标为(0,
,此时M点坐标为(0,![]() );
);
综上所述,M点的坐标为(0,![]() )或(0,
)或(0,![]() );
);
(3)连接DN,AD,如图,
∵AC=BC,CO⊥AB,
∴OC平分∠ACB,
∴∠ACO=∠BCO,
∵BD∥OC,
∴∠BCO=∠DBC,
∵DB=BC=AC=5,CM=BN,
∴△ACM≌△DBN,
∴AM=DN,
∴AM+AN=DN+AN,
而DN+AN≥AD(当且仅当点A、N、D共线时取等号),
∴DN+AN的最小值=![]() ,
,
∴AM+AN的最小值为![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
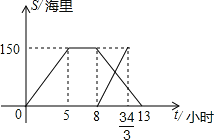
【题目】黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并。立即返航.渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离开港口的距离s和渔船离开港口的时间t之间的函数关系式
(2)求渔船与渔政船相遇对,两船与黄岩岛的距离、
(3在渔政船驶往黄岩岛的过程中,求渔船从港口 出发经过多长时间与渔政船相距30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,
,![]() 是数轴上一点,且
是数轴上一点,且![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,设运动时间为
个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
(1)数轴上点![]() 表示的数为 ,并用含
表示的数为 ,并用含![]() 的代数式表示点
的代数式表示点![]() 所表示的数为 ;
所表示的数为 ;
(2)设![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由,若不变,求线段
的长度是否发生变化?若变化,请说明理由,若不变,求线段![]() 的长度;
的长度;
(3)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,动点
个单位长度的速度沿数轴向左匀速运动,动点![]() 从点
从点![]() 出发,以点每秒
出发,以点每秒个单位长度沿数轴向左匀速运动,若
![]() 三点同时出发,在运动过程中,
三点同时出发,在运动过程中,![]() 到
到![]() 的距离,
的距离,![]() 到
到![]() 距离中,是否会有这两段距离相等的时候?若有,请求出此时的值;若没有,请说明理由.
距离中,是否会有这两段距离相等的时候?若有,请求出此时的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:![]() .
.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)有理数![]() 、
、![]() 、
、![]() 在数轴上的对应点如图所示,化简代数式:
在数轴上的对应点如图所示,化简代数式:![]()
![]()
(2)哈市某垃圾处理场一周处理生活垃圾任务为210吨,计划每天处理30吨,由于各种原因,实际每天处理量与计划相比有出入,某周七天的实际处理情况记录如下:
+6;-3;+4;-1;+2;-5;0
①垃圾场这一周实际处理生活垃圾是多少吨?
②若该垃圾场实行计量工资,每处理一吨生活垃圾给300元,同时又规定超额处理一吨垃圾另外奖100元,完不成任务的少处理一吨另外扣100元,那么该场工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com