
科目:初中数学 来源: 题型:
(1)如图1,平面内有一等腰直角三角板ABC(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,试证明线段AF,BF,CE之间的数量关系为AF+BF=2CE 。
(提示:过点C做BF的垂线,利用三角形全等证明。)
(2)若三角板绕点A顺时针旋转至图2的位置,其他条件不变,试猜想线段AF、BF、CE之间的数量关系,并证明你的猜想。
(3) 若三角板绕点A顺时针旋转至图3的位置,其他条件不变,则线段AF、BF、CE之间的数量关系为
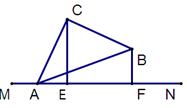
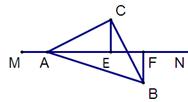
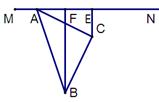
第22题图1 第22题图2 第22题图3
查看答案和解析>>
科目:初中数学 来源: 题型:
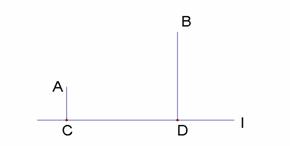
如图,A、B两个小镇在河流的同侧, 它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂向两镇供水,铺设水管的费用为每千米3万元。
它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂向两镇供水,铺设水管的费用为每千米3万元。
(1)请在河流上选择水 厂的位置M,使铺设水管的费用最少。(不写作法,保留作图痕迹)
厂的位置M,使铺设水管的费用最少。(不写作法,保留作图痕迹)
(2)最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图:在一张长为8cm,宽为6cm的长方形上,请画出三个形状大小不同的腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余两顶点在长方形的边上)。


查看答案和解析>>
科目:初中数学 来源: 题型:
某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x套,则根据题意可得方程为 ( )
(A)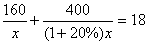 (B)
(B)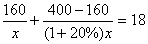
(C) 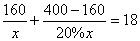 (D)
(D)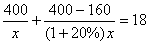
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com