
【题目】已如抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,﹣![]() )和(m﹣b,m2﹣mb+n),其中a,b,c,m,n为实数,且a,m不为0.
)和(m﹣b,m2﹣mb+n),其中a,b,c,m,n为实数,且a,m不为0.
(1)求c的值;
(2)求证:抛物线y=ax2+bx+c与x轴有两个交点;
(3)当﹣1≤x≤1时,设抛物线y=ax2+bx+c与x轴距离最大的点为P(x0,y0),求这时|y0|的最小值.
【答案】(1)c=![]() ;(2)见解析;(3)当b=0,x0=0时,这时|yo|取最小值,为|yo|=
;(2)见解析;(3)当b=0,x0=0时,这时|yo|取最小值,为|yo|=![]()
【解析】
(1)将(0,![]() )代入抛物线y=ax2+bx+c中即可;
)代入抛物线y=ax2+bx+c中即可;
(2)先求n的值,再将点的坐标(m-b,m2-mb+n)代入y=ax2+bx+c中,计算△>0即可;
(3)先根据公式分别求抛物线的对称轴和最小值,分四种情况进行讨论:
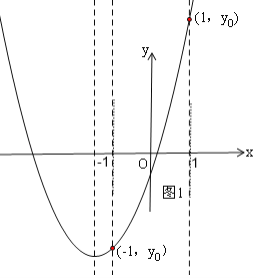
①当![]() <-1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),在x轴下方与x轴距离最大的点是(-1,yo),代入抛物线的解析式中分别求|H|和|h|,作判断即可;
<-1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),在x轴下方与x轴距离最大的点是(-1,yo),代入抛物线的解析式中分别求|H|和|h|,作判断即可;
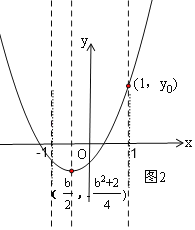
②当-1≤![]() ≤0,即0≤b≤2时,如图2,
≤0,即0≤b≤2时,如图2,
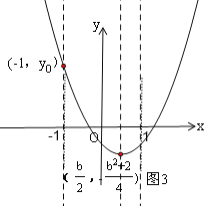
③当0<![]() ≤1,即-2≤b<0时,如图3,
≤1,即-2≤b<0时,如图3,
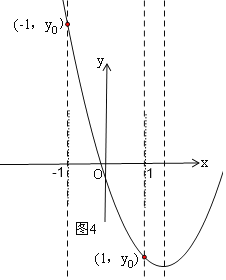
④当1<![]() ,即b<-2时,如图4,
,即b<-2时,如图4,
根据图象分别求其y0的取值范围,可得结论.
解:(1)∵(0,![]() )在y=ax2+bx+c上,
)在y=ax2+bx+c上,
∴![]() =a×02+b×0+c,
=a×02+b×0+c,
∴c=![]() ;
;
(2)又可得 n=![]() ,
,
∵点(m﹣b,m2﹣mb+n)在y=ax2+bx+c上,
∴m2﹣mb![]() =a(m﹣b)2+b(m﹣b)
=a(m﹣b)2+b(m﹣b)![]() ,
,
∴(a﹣1)(m﹣b)2=0,
若(m﹣b)=0,则(m﹣b,m2﹣mb+n)与(0,![]() )重合,与题意不合,
)重合,与题意不合,
∴a=1,
∴抛物线y=ax2+bx+c,就是y=x2+bx﹣![]() ,
,
△=b2﹣4ac=b2﹣4×(![]() )=b2+2>0,
)=b2+2>0,
∴抛物线y=ax2+bx+c与x轴有两个交点;
(3)抛物线y=x2+bx![]() 的对称轴为
的对称轴为![]() ,最小值为
,最小值为![]() ,
,
设抛物线y=x2+bx![]() 在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h,
在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h,
①当![]() <﹣1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),
<﹣1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),
∴|H|=yo=![]() +b>
+b>![]() ,
,
在x轴下方与x轴距离最大的点是(﹣1,yo),
∴|h|=|yo|=|![]() ﹣b|=b﹣
﹣b|=b﹣![]() >
>![]() ,
,
∴|H|>|h|,
∴这时|yo|的最小值大于![]() ;
;
②当﹣1≤![]() ≤0,即0≤b≤2时,如图2,在x轴上方与x轴距离最大的点是(1,yo),
≤0,即0≤b≤2时,如图2,在x轴上方与x轴距离最大的点是(1,yo),
∴|H|=yo=![]() +b≥
+b≥![]() ,当b=0时等号成立.
,当b=0时等号成立.
在x轴下方与x轴距离最大的点是![]() ,
,
∴|h|=|![]() |=
|=![]() ≥
≥![]() ,当b=0时等号成立.
,当b=0时等号成立.
∴这时|yo|的最小值等于![]() .
.
③当0<![]() ≤1,即﹣2≤b<0时,如图3,在x轴上方与x轴距离最大的点是
≤1,即﹣2≤b<0时,如图3,在x轴上方与x轴距离最大的点是
(﹣1,yo),
∴|H|=yo=1+(﹣1)b﹣![]() =
=![]() ﹣b>
﹣b>![]() ,在x轴下方与x轴距离最大的点是
,在x轴下方与x轴距离最大的点是 ![]() ,
,
∴|h|=|yo|=|![]() |=
|=![]() >
>![]() .
.
∴这 时|yo|的 最 小 值 大 于![]() .
.
④当1<![]() ,即b<﹣2时,如图4,在x轴上方与x轴距离最大的点是(﹣1,yo),
,即b<﹣2时,如图4,在x轴上方与x轴距离最大的点是(﹣1,yo),
∴|H|=![]() ﹣b>
﹣b>![]() ,在x轴下方与x轴距离最大的点是(1,yo),
,在x轴下方与x轴距离最大的点是(1,yo),
∴|h|=|![]() +b|=﹣(b+
+b|=﹣(b+![]() )>
)>![]() ,
,
∴|H|>|h|,
∴这时|yo|的最小值大于![]() ,
,
综上所述,当b=0,x0=0时,这时|yo|取最小值,为|yo|=![]() .
.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
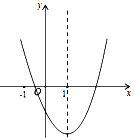
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2﹣b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的有_______.(填所以正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,直接写出抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,请用列表法或树状图法,求抽到的都是合格品的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在半径为25cm的⊙O中,弦AB=40cm,则弦AB所对的弧的中点到AB的距离是( )
A.10cmB.15cmC.40cmD.10cm或40cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com