

分析 (1)过点P作MN∥BC,分别交AB、CD于点M、N,根据矩形的性质和直角三角形的性质,可证明△QNP≌△PMB,可证明PQ=PB;
(2)△PCQ可以成为等腰三角形.当点Q在DC边上时,利用勾股定理可得到x的方程;
当点Q在DC的延长线上时,由PQ=CQ,可得到x的方程;从而可求得满足条件的x的值.
解答 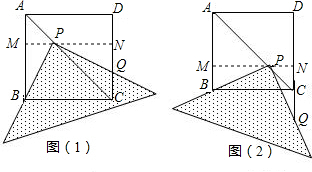 解:(1)PB=PQ.
解:(1)PB=PQ.
证明:过P作MN∥BC,分别交AB、DC于点M、N,则四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰直角三角形(如图1).
∴NP=NC=MB.
∵∠BPQ=90°,
∴∠QPN+∠BPM=90°.
而∠PBM+∠BPM=90°,
∴∠QPN=∠PBM.
又∵∠QNP=∠PMB=90°,
∴△QNP≌△PMB.∴PB=PQ.
(2)△PCQ可能成为等腰三角形.
①方法一、当点P与点A重合时,点Q与点D重合,
这时PQ=QC,△PCQ是等腰三角形.
此时x=0.
方法二、当点Q在边DC上,
由PQ2=CQ2得:(1-$\frac{\sqrt{2}}{2}$x)2+($\frac{\sqrt{2}}{2}$x)2=(1-$\sqrt{2}$x)2
解得x1=0,x2=$\sqrt{2}$(舍去);
②解法一:当点Q在边DC的延长线上,且CP=CQ时,△PCQ是等腰三角形(如图2).
此时,QN=PM=$\frac{{\sqrt{2}}}{2}x$,CP=$\sqrt{2}-x$,CN=$\frac{{\sqrt{2}}}{2}$CP=1-$\frac{{\sqrt{2}}}{2}x$.
∴CQ=QN-CN=$\frac{{\sqrt{2}}}{2}x-({1-\frac{{\sqrt{2}}}{2}x})=\sqrt{2}x-1$.
此时,得x=1.
解法二:当点Q在边DC的延长线上,且CP=CQ时,△PCQ是等腰三角形(如图2).
由于此时,∠CPQ=$\frac{1}{2}$∠PCN=22.5°,
∴∠APB=90°-22.5°=67.5°,∠ABP=180°-(45°+67.5°)=67.5°.
∴∠APB=∠ABP.
∴AP=AB=1.
∴x=1.
故当点P在线段AC上滑动时,△PCQ可能成为等腰三角形.
点评 本题主要考查四边形的综合应用,涉及正方形的性质、全等三角形的判定和性质、直角三角形的性质、等腰三角形的性质和勾股定理等知识.在(2)中利用分类讨论思想分别得到关于x的方程是解题的关键.本题考查知识点较多,综合性较强,有一定的难度.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
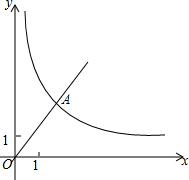 已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 存在三角形使得p=1或p=2 | B. | 0<p<1 | ||
| C. | 1<p<2 | D. | 2<p<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{V}$=$\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$ | B. | $\frac{m}{V}$>$\frac{{m}_{1}}{{V}_{1}}$>$\frac{{m}_{2}}{{V}_{2}}$ | ||
| C. | $\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$≤$\frac{m}{V}$ | D. | $\frac{{m}_{2}}{{V}_{2}}$=$\frac{{m}_{1}}{{V}_{1}}$≥$\frac{m}{V}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com