【题目】如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°， 则∠BAC的度数为（ ）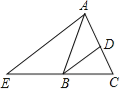
A. 40° B. 45° C. 60° D. 70°
阅读快车系列答案科目：初中数学 来源： 题型：
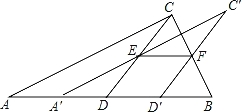
【题目】(2016湖南省邵阳市第10题)如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(2016云南省第23题)有一列按一定顺序和规律排列的数：
第一个数是
；
第二个数是
；
第三个数是
；
…
对任何正整数n，第n个数与第（n+1）个数的和等于
．
（1）经过探究，我们发现：
设这列数的第5个数为a，那么
，
，
，哪个正确？
请你直接写出正确的结论；
（2）请你观察第1个数、第2个数、第3个数，猜想这列数的第n个数（即用正整数n表示第n数），并且证明你的猜想满足“第n个数与第（n+1）个数的和等于”；
（3）设M表示
，
，
，…，
，这2016个数的和，即
，
求证：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面给出了四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能判定四边形ABCD是平行四边形的是（ ）
A.1：2：3：4
B.2：2：3：3
C.2：3：2：3
D.2：3：3：2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．
（1）求证：∠ACD=∠B；
（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；
①求tan∠CFE的值；
②若AC=3，BC=4，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
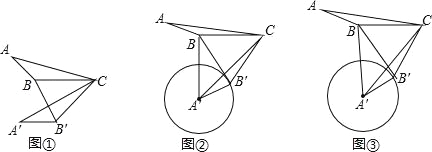
【题目】数学活动﹣旋转变换
（1）如图①，在△ABC中，∠ABC=130°，将△ABC绕点C逆时针旋转50°得到△A′B′C，连接BB′，求∠A′B′B的大小；
（2）如图②，在△ABC中，∠ABC=150°，AB=3，BC=5，将△ABC绕点C逆时针旋转60°得到△A′B′C，连接BB′，以A′为圆心，A′B′长为半径作圆．
（Ⅰ）猜想：直线BB′与⊙A′的位置关系，并证明你的结论；
（Ⅱ）连接A′B，求线段A′B的长度；
（3）如图③，在△ABC中，∠ABC=α（90°＜α＜180°），AB=m，BC=n，将△ABC绕点C逆时针旋转2β角度（0°＜2β＜180°）得到△A′B′C，连接A′B和BB′，以A′为圆心，A′B′长为半径作圆，问：角α与角β满足什么条件时，直线BB′与⊙A′相切，请说明理由，并求此条件下线段A′B的长度（结果用角α或角β的三角函数及字母m、n所组成的式子表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
