
【题目】数学活动﹣旋转变换
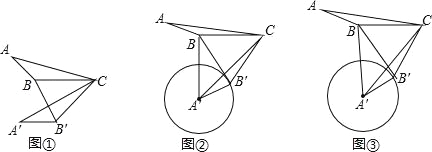
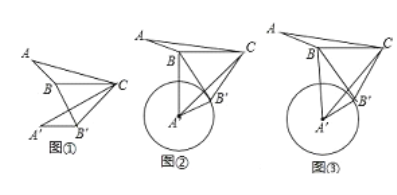
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
【答案】(1)65°;(2)(Ⅰ)结论:直线BB′、是⊙A′的切线,理由详见解析;(Ⅱ)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由旋转的性质可得∠A′B′C=∠ABC=130°,CB=CB′,根据等腰三角形的性质和三角形的内角和定理即可求得∠A′B′B得度数;(2)(Ⅰ)结论:直线BB′是⊙A′的切线.根据已知条件证明∠A′B′B=90°,即可判定直线BB′是⊙A′的切线;(Ⅱ)在RT△ABB′中,根据勾股定理即可计算出线段A′B的长度;(3)如图③中,当α+β=180°时,直线BB′、是⊙A′的切线.只要证明∠A′B′B=90°即可解决问题.在△CBB′中求出BB′,再在RT△A′B′B中利用勾股定理即可.
试题解析:(1)如图①中,∵△A′B′C是由△ABC旋转得到,
∴∠A′B′C=∠ABC=130°,CB=CB′,
∴∠CBB′=∠CB′B,∵∠BCB′=50°,
∴∠CBB′=∠CB′B=65°,
∴∠A′B′B=∠A′B′C﹣∠BB′C=65°.
(2)(Ⅰ)结论:直线BB′、是⊙A′的切线.
理由:如图②中,∵∠A′B′C=∠ABC=150°,CB=CB′,
∴∠CBB′=∠CB′B,∵∠BCB′=60°,
∴∠CBB′=∠CB′B=60°,
∴∠A′B′B=∠A′B′C﹣∠BB′C=90°.
∴AB′⊥BB′,
∴直线BB′是⊙A′的切线.
(Ⅱ)∵在RT△ABB′中,∵∠AB′B=90°,BB′=BC=5,AB′=AB=3,
∴A′B=![]() =
=![]() .
.
(3)如图③中,当α+β=180°时,直线BB′、是⊙A′的切线.
理由:∵∠A′B′C=∠ABC=α,CB=CB′,
∴∠CBB′=∠CB′B,∵∠BCB′=2β,
∴∠CBB′=∠CB′B=![]() ,
,
∴∠A′B′B=∠A′B′C﹣∠BB′C=α﹣90°+β=180°﹣90°=90°.
∴AB′⊥BB′,
∴直线BB′、是⊙A′的切线.
在△CBB′中∵CB=CB′=n,∠BCB′=2β,
∴BB′=2nsinβ,
在RT△A′BB′中,A′B=![]() =
=![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°, 则∠BAC的度数为( )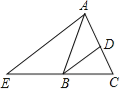
A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
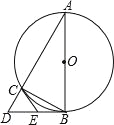
【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一些分别标有-1,2,-4,8,-16,32,…的卡片,这些卡片上的数字是按一定规律排列的,小明拿到了相邻的三张卡片,且卡片上的数字之和为96,则小明拿到的三张卡片上分别标有什么数字?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面几种说法:①对角线互相垂直的四边形是菱形;②一组对边平行,一组邻边相等的四边形是菱形;③对角线相等的平行四边形是矩形;④对角线互相垂直平分的四边形是菱形,那么准确的说法是( )
A.①②③B.②③C.③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对小丽说:“请你任意想一个数,把这个数乘2后加12,然后除以6,再减去你原来所想的那个数与6的差的三分之一,我可以知道你计算的结果.”请你根据小明的说法探索:
(1)如果小丽一开始想的那个数是-5,请列式并计算结果;
(2)如果小丽一开始想的那个数是![]() ,请列式并计算结果;
,请列式并计算结果;
(3)根据(1)、(2),尝试写出一个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com