
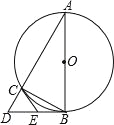
【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据弦切角定理和切线的性质可得∠CBE=∠A,∠ABD=90°,根据圆周角定理可得∠ACB=90°,即可得∠ACO+∠BCO=90°,∠BCD=90°,再由直角三角形斜边上的中线性质得出CE=![]() BD=BE,根据等腰三角形的性质可得∠BCE=∠CBE=∠A,即可证出∠ACO=∠BCE,所以∠BCE+∠BCO=90°,即CE⊥OC,所以CE是⊙O的切线;(2)由勾股定理求出AB的长,再由三角函数得出tanA=
BD=BE,根据等腰三角形的性质可得∠BCE=∠CBE=∠A,即可证出∠ACO=∠BCE,所以∠BCE+∠BCO=90°,即CE⊥OC,所以CE是⊙O的切线;(2)由勾股定理求出AB的长,再由三角函数得出tanA=![]() =
=![]() ,求出BD=
,求出BD=![]() AB=
AB=![]() ,即可得出CE的长.
,即可得出CE的长.
试题解析:(1)证明:连接OC,如图所示:
∵BD是⊙O的切线,
∴∠CBE=∠A,∠ABD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,∠BCD=90°,
∵E是BD中点,
∴CE=![]() BD=BE,
BD=BE,
∴∠BCE=∠CBE=∠A,
∵OA=OC,
∴∠ACO=∠A,
∴∠ACO=∠BCE,
∴∠BCE+∠BCO=90°,
即∠OCE=90°,CE⊥OC,
∴CE是⊙O的切线;
(2)解:∵∠ACB=90°,
∴AB=![]() ,
,
∵tanA=![]() =
=![]() ,
,
∴BD=![]() AB=
AB=![]() ,
,
∴CE=![]() BD=
BD=![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
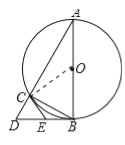
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.

解:∠B+∠E=∠BCE
过点C作CF∥AB,
则![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动﹣旋转变换
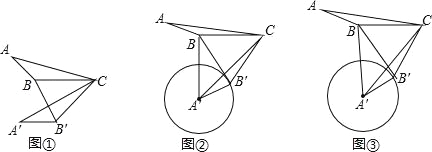
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让市民享受到更多的优惠,某市针对乘坐地铁的人群进行了调查.
(1)为获得乘坐地铁人群的月均花费信息,下列调查方式中比较合理是 ;
A.对某小区的住户进行问卷调查 B.对某班的全体同学进行问卷调查
C.在市里的不同地铁站,对进出地铁的人进行问卷调查
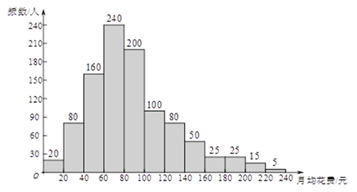
(2)调查小组随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了
频数分布直方图,如图所示.
① 根据图中信息,估计平均每人乘坐地铁的月均花费的范围是 元;
A.20—60 B.60—120 C.120—180
②你是用_________(填统计概念)对①进行估计的。
③为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.根据图中信息,乘坐地铁的月均花费达到 元的人可以享受扣.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在选取样本时,下列说法不正确的是( )
A. 所选样本必须足够大 B. 所选样本要具有代表性
C. 所选样本可按自己的爱好抽取 D. 仅仅增加调查人数不一定能提高调查质量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com