
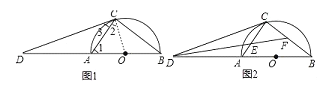
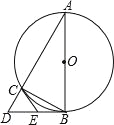
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据切线的性质、直径所对的圆周角是直角及等角的余角相等即可证明结论.
(2)①由∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,即可得∠CEF=∠CF,再由∠ECF=90°,可得∠CEF=∠CFE=45°,即可得结论.
②由勾股定理可求得AB=5,根据已知易证△DCA∽△DBC,得![]() ,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得
,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得![]() ,设EC=CF=x,列出方程即可解决问题.
,设EC=CF=x,列出方程即可解决问题.
试题解析:(1)证明:如图1中,连接OC.
∵OA=OC,
∴∠1=∠2,
∵CD是⊙O切线,
∴OC⊥CD,
∴∠DCO=90°,
∴∠3+∠2=90°,
∵AB是直径,
∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,
∴∠CEF=∠CFE,∵∠ECF=90°,
∴∠CEF=∠CFE=45°,
∴tan∠CFE=tan45°=1.
②在RT△ABC中,∵AC=3,BC=4,
由勾股定理得AB=5,
∵∠CDA=∠BDC,∠DCA=∠B,
∴△DCA∽△DBC,
∴![]() ,设DC=3k,DB=4k,
,设DC=3k,DB=4k,
∵CD2=DADB,
∴9k2=(4k﹣5)4k,
∴k=![]() ,
,
∴CD=![]() ,DB=
,DB=![]() ,
,
∵∠CDE=∠BDF,∠DCE=∠B,
∴△DCE∽△DBF,
∴![]() ,设EC=CF=x,
,设EC=CF=x,
∴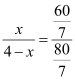 ,
,
∴x=![]() .
.
∴CE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°, 则∠BAC的度数为( )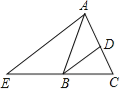
A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)根据上面算式的规律,请计算:1+3+5+…+199=________;
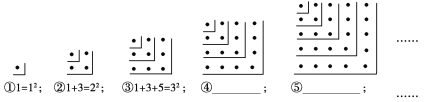
(3)请你用代数式表示出上面规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当人用眼睛看其他事物时,人眼睛的位置称为________,由________发出的射线称为________.人的眼睛看不到的地方称为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对小丽说:“请你任意想一个数,把这个数乘2后加12,然后除以6,再减去你原来所想的那个数与6的差的三分之一,我可以知道你计算的结果.”请你根据小明的说法探索:
(1)如果小丽一开始想的那个数是-5,请列式并计算结果;
(2)如果小丽一开始想的那个数是![]() ,请列式并计算结果;
,请列式并计算结果;
(3)根据(1)、(2),尝试写出一个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com