
【题目】若等腰三角形中有一个角等于36°,则这个等腰三角形的顶角的度数为( )
A. 36° B. 72° C. 108°或36° D. 108°或72°
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E,
(1)求证:CF=CG;
(2)连接DE,若BE=4CE,CD=2求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在A′处,BC为折痕.
(1)图①中,若∠1=30![]() ,求∠A′BD的艘数;
,求∠A′BD的艘数;
(2)如果将图①的另一角∠A′BD斜折过去,使BD边与BA′重合,折痕为BE,点D的对应点为D′,如图②所示.∠1=30![]() ,求∠2以及∠CBE的度数;
,求∠2以及∠CBE的度数;
(3)如果将图①的另一角斜折过去,使BD边落在∠l内部,折痕为BE,点D的对应点为D′,如图③所示,若∠1=40![]() ,设∠A′BD′=α,∠EBD=β,请直接回答:
,设∠A′BD′=α,∠EBD=β,请直接回答:
①α的取值范围和β的取值范围:
②α与β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )

①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③∠BOC+∠AOD=180°;
④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣1)2+4,
(1)求出二次函数的顶点坐标及与x轴交点坐标,结合开口方向再在网格中画出草图.

(2)观察图象确定:x取何值时,y随着x的增大而增大,当X取何值时,y随着x的增大而减少.
(3)观察图象确定:x取何值时y>0,x取何值时y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2 , 也可表示为c3+4(![]() ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4(![]() ab)由此推导出一个重要的结论a2+b2=c2 , 这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推导出一个重要的结论a2+b2=c2 , 这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.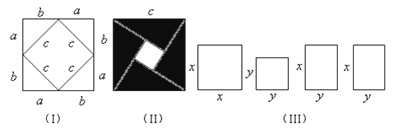
(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( ) 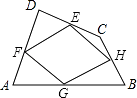
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平脉直角坐标系中,已知点A(2﹣a,2a+3)在第四象限.
(1)若点A到x轴的距离与到y轴的距离相等,求a的值;
(2)若点A到x轴的距离小于到y轴的距离,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪些线段能组成三角形( )
①3cm、3cm、5cm ②3cm、3cm、3cm ③2cm、2cm、4cm ④3cm、5cm、9cm
A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com