
����Ŀ���ڷ��ʹ������������Ļ�У������γ�����ȵIJ�ɫ��ש�������ֱ��ס�������ʩ����ͬʱ����ʩ������ͼ�Ƿ�ӳ�������ɫ��ש�ij���y���ף���ʩ��ʱ��x��ʱ��֮���ϵ�IJ���ͼ�������������⣺
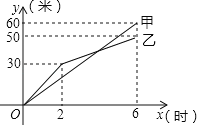
��1�����Ҷ���2��x��6��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
��2�������ʩ���ٶȲ��䣬�Ҷ��ڿ���6Сʱ��ʩ���ٶ����ӵ�12��/ʱ���������ͬʱ�����������Ӵӿ�ʼʩ�����깤������IJ�ɫ��ש�ij���Ϊ�����ף�
���𰸡���1��y=5x+20����2��110�ף�
��������
��1���躯����ϵʽΪy=kx+b��Ȼ�����ô���ϵ������һ�κ�������ʽ���
��2��������ӵ��ٶȣ�Ȼ����Ӵӿ�ʼ���깤�������ɫ��ש�ij���Ϊz�ף��ٸ���6Сʱ�����ӵ�ʩ��ʱ������г�������⼴�ɣ�
�⣺��1�����Ҷ���2��x��6��ʱ����y��x֮��ĺ�����ϵʽΪy=kx+b��
��ͼ��֪������ͼ����㣨2��30������6��50����
��![]() ��
��
���![]() ��
��
��y=5x+20��
��2����ͼ��֪�����ٶ��ǣ�60��6=10����/ʱ����
��Ӵӿ�ʼ���깤�������ɫ��ש�ij���Ϊz�ף�
�����⣬��![]() ��
��
���z=110��
�𣺼Ӵӿ�ʼ���깤�������ɫ��ש�ij���Ϊ110�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
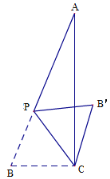
����Ŀ����ͼ������ABC �У���ACB��90����AC��12��BC��5��P �DZ� AB �ϵĶ��㣨����� B �غϣ�������BCP �� CP ���ڵ�ֱ�߷��ۣ��õ���B��CP������ B��A��B��A ���ȵ���Сֵ�� m��B��A ���ȵ����ֵ�� n���� m+n ��ֵ���� ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
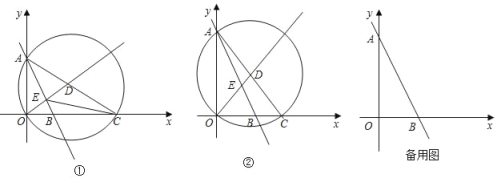
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y����2x+4�������ύ��A��B���㣬����C��x���������ϣ���DΪ��AOC�����Բ������OD��ֱ��AB���ڵ�E��
��1����ͼ�٣���OE��DE����![]() ��ֵ��
��ֵ��
��2����ͼ�ڣ�����ABC��2��ACBʱ����OC�ij���
��3����C��ԭ����x���������˶������У���OC�ij�Ϊa��
���ú�a�Ĵ���ʽ��ʾ��E�ĺ�����xE������xE��BC����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
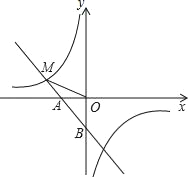
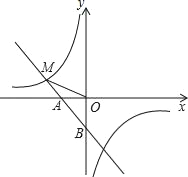
����Ŀ����ͼ��һ�κ���y1����x��1��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B���뷴��������![]() ͼ���һ������ΪM����2��m����
ͼ���һ������ΪM����2��m����
��1�����������Ľ���ʽ��
��2����y2��y1ʱ����x��ȡֵ��Χ��
��3�����B��ֱ��OM�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1����x��1��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B���뷴��������![]() ͼ���һ������ΪM����2��m����
ͼ���һ������ΪM����2��m����
��1�����������Ľ���ʽ��
��2����y2��y1ʱ����x��ȡֵ��Χ��
��3�����B��ֱ��OM�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���O��б��AB�ϣ���OΪԲ�ģ�OBΪ�뾶��Բ���ֱ���BC��AB�ཻ�ڵ�D��E������AD����֪��CAD=��B,
��1����֤��AD�ǡ�O�����ߣ�
��2����BC=8��tanB=![]() �����O �İ뾶��
�����O �İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲO�İ뾶��Ϊ2����A��B��CΪԲO�����㣬��BC=AO����DΪBC���е㣬
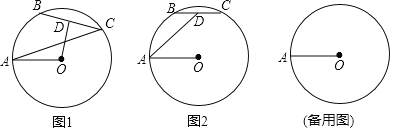
(1)��ͼ������AC��OD�����OAC=������������ʾ��AOD��
(2)��ͼ������BΪ![]() ���е�ʱ�����A��D֮��ľ��룺
���е�ʱ�����A��D֮��ľ��룺
(3)���AD���ӳ�����ԲO���ڵ�E����OΪԲ�ģ�ADΪ�뾶��Բ����BCΪֱ����Բ���У�����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2014��ʦ��Ƹ��������Ļ������ܶ���־�ڽ�����ҵ����Ա�ܶ���ᣮ�����ǽ��걨������ͳ�Ʊ�����ѧ��
��Ƹ��λ | ��Ƹ�ƻ� | �������� | |||
���н�ʦ1 | �о��� | ���� | ��ѧ | 10 | |
���н�ʦ2 | ��ͨ | ���� | ��ѧ | 19 | |
���н�ʦ | ��ͨ | ���� | ��ѧ | 12 | 55 |
Сѧ��ʦ1 | ��ͨ | ��������� | ��ѧ | 18 | 83 |
Сѧ��ʦ2 | ��ͨ | ���� | ��ѧ | 21 | 93 |
��1�������ϱ���Ϣ���������������������ͳ��ͼ����������
��2��¼ȡ������С���Ƕ��٣������Ƕ��٣�
��3��������㣨���Ʊ�ҵ��������¼ȡ�����Ͽ������ѡ���ĸ���λ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ݳ��Ṻ����Ʊ�ķ�ʽ�����֣�
��ʽһ������λ��������10��Ԫ����õ�λ������Ʊ�ļ۸�Ϊÿ��0.02��Ԫ��
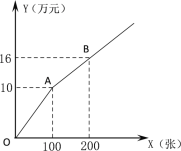
��ʽ������ͼ��ʾ��
�蹺����Ʊx�ţ��ܷ���Ϊy��Ԫ����ʽһ�У��ܷ���=���������+��Ʊ�ѣ�
��1����ʽһ��y��x�ĺ�����ϵʽ��
��2�����ס���������λ�ֱ���÷�ʽһ����ʽ�������ݳ�����Ʊ��400�ţ����ҵ�λ����100�ţ�����λ������27.2��Ԫ����ס�������λ��������Ʊ�����ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com