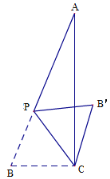
[题目]如图.在△ABC 中.∠ACB＝90°.AC＝12.BC＝5.P 是边 AB 上的动点(不与点 B 重合).将△BCP 沿 CP 所在的直线翻折.得到△B＇CP.连接 B＇A.B＇A 长度的最小值是 m.B＇A 长度的最大值是 n.则 m+n 的值等于．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在△ABC 中，∠ACB＝90°，AC＝12，BC＝5，P 是边 AB 上的动点（不与点 B 重合），将△BCP 沿 CP 所在的直线翻折，得到△B＇CP，连接 B＇A，B＇A 长度的最小值是 m，B＇A 长度的最大值是 n，则 m+n 的值等于 ______．

【答案】24

【解析】

先判断出B′A长度的最大值和B′A长度的最小值的位置，最后简单计算即可．

解：如图，

∵点P是直线AB上的动点，
∴△BCP沿CP所在的直线翻折得到△B'CP，点B落在以点C为圆心，BC为半径的圆上，延长AC交圆于M，
圆外一点到圆上的点的距离最大和最小的点是圆外一点过圆心的直线和圆的交点，
∴CM=CN=BC=6，

∴B′A长度的最小值是m=AN=AC-CN=12-5=7，
B′A长度的最大值是n=AM=AC+CM=12+5=17，
∴m+n=7+17=24；
故答案为24．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

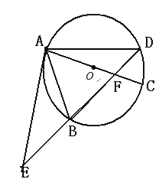
【题目】（本题满分8分）如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上一点，

∠EAB=∠ADB.

（1）求证：EA是⊙O的切线；

（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；

（3）在（2）的条件下，已知AF=4，CF=2，求AE的长.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知二次函数（是常数，）图象的对称轴是直线，其图象的一部分如图所示，下列说法中①；②；③当时，；④；⑤．正确的结论有（）

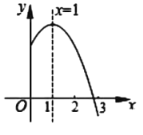
A.①②④B.②③④C.①③⑤D.①②③④⑤

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】北京地铁票价计费标准如下表所示：

乘车距离（公里）
票价（元）	3	4	5	6	每增加1元可乘坐20公里

另外，使用市政交通一卡通，每个自然月每张卡片支出累计满100元后，超出部分打8折；满150元后，超出部分打5折；支出累计达400元后，不再打折．小红妈妈上班时，需要乘坐地铁15公里到达公司，每天上下班共乘坐两次．如果每次乘坐地铁都使用市政交通一卡通，那么每月第21次乘坐地铁上下班时，她刷卡支出的费用（　　）

A.2.5元B.3元C.4元D.5元

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某公司计划投资万元引进一条汽车配件流水生产线，经过调研知道该流水生产线的年产量为件，每件总成本为万元，每件出厂价万元；流水生产线投产后，从第年到第年的维修、保养费用累计(万元)如下表：

第年							···
维修、保养费用累计万元							···

若上表中第年的维修、保养费用累计(万元)与的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个．

（1）求出关于的函数解析式；

（2）投产第几年该公司可收回万元的投资？

（3）投产多少年后，该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)？

查看答案和解析>>

科目：初中数学 来源： 题型：

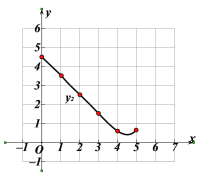
【题目】如图，矩形ABCD的对角线上有动点E，连结DE，边BC上有一定点F，连接EF，已知AB=3cm，AD=4cm，设A，E两点间的距离为cm，D，E两点间的距离为cm，E，F两点间的距离为cm．

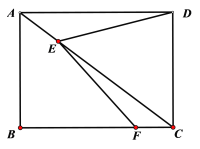
小胜根据学习函数的经验，分别对函数，随自变量x的变化而变化的规律进行了探究．下面是小胜的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，得到x与y的几组对应值：

x/cm	0	1	2	3	4	5
/cm	4.00	3.26	2.68	_______	2.53	3.00
/cm	4.50	3.51	2.51	1.53	0.62	0.65

（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点，并画出函数的图像：

（3）结合函数图像，解决问题：当DE>EF时，AE的长度范围约为_________________cm．

查看答案和解析>>

科目：初中数学 来源： 题型：

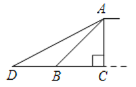
【题目】某市为了缓解城市交通压力，决定修建人行天桥，原设计天桥的楼梯与地面的夹角为45°（∠ABC=45°），BC=4.2 m，后考虑安全因素，将楼梯角B移到CB的延长线上点D处，使∠ADC=23°（如图所示）．求BD的长(精确到0.1 m)．（参考数据：sin 67°≈0.92，cos 67°≈0.39，tan 67°≈2.36）