Question

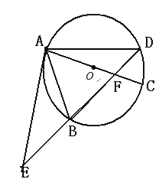
【题目】（本题满分8分）如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上一点，

∠EAB=∠ADB.

（1）求证：EA是⊙O的切线；

（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；

（3）在（2）的条件下，已知AF=4，CF=2，求AE的长.

Answer 1

【答案】（1）见解析；（2）见解析；（3）AE=4

【解析】试题分析：（1）连接CD，根据直径所对的圆周角为直角得出∠ADB+∠EDC=90°，根据同弧所对的圆周角相等得出∠BAC=∠EDC，然后结合已知条件得出∠EAB+∠BAC=90°，从而说明切线；（2）连接BC，根据直径的性质得出∠ABC=90°，根据B是EF的中点得出AB=EF，即∠BAC=∠AFE，则得出三角形相似；（3）根据三角形相似得出，根据AF和CF的长度得出AC的长度，然后根据EF=2AB代入求出AB和EF的长度，最后根据Rt△AEF的勾股定理求出AE的长度．

试题解析：（1）证明：如答图1，连接CD， ∵AC是⊙O的直径，∴∠ADC=90°．

∴∠ADB+∠EDC=90°．

∵∠BAC=∠EDC，∠EAB=∠ADB， ∴∠BAC=∠EAB+∠BAC=90°．∴EA是⊙O的切线．

（2）证明：如答图2，连接BC， ∵AC是⊙O的直径，∴∠ABC=90°．∴∠CBA=∠ABC=90°．

∵B是EF的中点，∴在Rt△EAF中，AB=BF． ∴∠BAC=∠AFE． ∴△EAF∽△CBA．

（3）∵△EAF∽△CBA，∴． ∵AF=4，CF=2， ∴AC=6，EF=2AB．

∴，解得AB=2．∴EF=4．

∴AE=．