
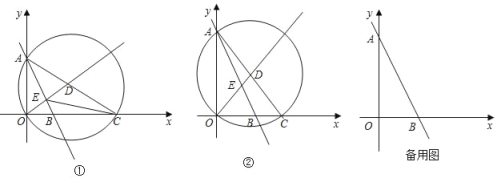
【题目】如图,在平面直角坐标系中,直线y=﹣2x+4与坐标轴交于A,B两点,动点C在x轴正半轴上,⊙D为△AOC的外接圆,射线OD与直线AB交于点E.
(1)如图①,若OE=DE,求![]() 的值;
的值;
(2)如图②,当∠ABC=2∠ACB时,求OC的长;
(3)点C由原点向x轴正半轴运动过程中,设OC的长为a,
①用含a的代数式表示点E的横坐标xE;②若xE=BC,求a的值.
【答案】(1)![]() ;(2)OC=2
;(2)OC=2![]() ﹣2;(3)①xE=
﹣2;(3)①xE=![]() ;②a的值为
;②a的值为![]() ±1.
±1.
【解析】
(1)根据三角形的面积公式计算;
(2)作OF⊥AC于点F,根据一次函数的性质求出OA、OB,根据正切的定义得到tan∠ODC=2,设DF=m,根据勾股定理用m表示出OD,计算即可;
(3)①作EH⊥AO于点H,根据相似三角形的性质列式计算,得到答案;
②分C在点B右侧、C在点B左侧两种情况,分别列出方程,解方程即可.
(1)∵OE=DE,
∴S△AOE=S△ADE,
∵AD=CD,
∴S△CDE=S△ADE,
∴![]() ,
,
故答案为:![]() ;
;
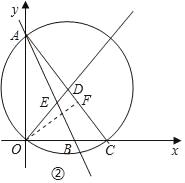
(2)作OF⊥AC于点F,
对于直线y=﹣2x+4,当y=0时,x=2,当x=0时,y=4,
则A的坐标为(0,4),点B的坐标为(2,0),即OA=4,OB=2,
∵∠ABC=2∠ACB,
∴∠ADO=∠ABC,
∴∠ODC=∠ABO,
∴tan∠ODC=tan∠ABO=2,
设DF=m,则OF=2m,
由勾股定理得,OD=![]() m,
m,
∴CF=(![]() ﹣1)m,
﹣1)m,
∴tan∠OCD=![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,OC=2![]() ﹣2;
﹣2;
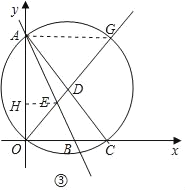
(3)①设直线OD交⊙D另一点为G,连结AG,作EH⊥AO于点H,
则EH∥AG,
∴![]() ,
,![]() ,
,
∴![]() =1,即
=1,即![]() =1,
=1,
解得,xE=![]() ;
;
②当C在点B右侧时,BC=xE,即a﹣2=xE,
∴a﹣2=![]() ,
,
解得,a1=1+![]() ,a2=1﹣
,a2=1﹣![]() (舍去),
(舍去),
当C在点B左侧时,BC=xE,即2﹣a=xE,
∴2﹣a=![]() ,
,
解得,a1=﹣1+![]() ,a2=﹣1﹣
,a2=﹣1﹣![]() (舍去),
(舍去),
所以a的值为![]() ±1.
±1.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,﹣2),OB=4OA,tan∠BCO=2.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M、N分别是线段BC、AB上的动点,点M从点B出发以每秒![]() 个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?
个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
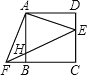
【题目】如图,△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,则下列结论: ①AE⊥AF;②EF:AF=![]() :1;③AF2=FHFE;④FB:FC=HB:EC.正确的是___.
:1;③AF2=FHFE;④FB:FC=HB:EC.正确的是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
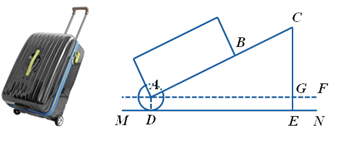
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 轴相交于点
轴相交于点![]() ,抛物线与
,抛物线与![]() 轴相交于点
轴相交于点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;

(3)如图2,点![]() 是折线
是折线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,直线
轴,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 落在
落在![]() 轴上,请直接写出
轴上,请直接写出![]() 点的坐标.
点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
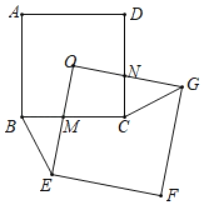
【题目】如图,已知正方形OEFG的顶点O与正方形ABCD的中心O重合,若正方形OEFG绕O点旋转.
(1)探究:在旋转的过程中线段BE与线段CG有什么数量关系及位置关系?证明你的结论;
(2)若正方形ABCD的边长为a,探究:在旋转过程中四边形OMCN的面积是否发生变化?若不变化求其面积,若变化指出变化过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
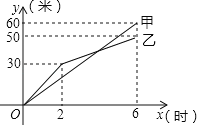
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
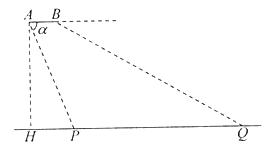
【题目】如图,从一架水平飞行的无人机![]() 的尾端点
的尾端点![]() 测得正前方的桥的左端点
测得正前方的桥的左端点![]() 俯角为
俯角为![]() ,且
,且![]() ,无人机的飞行高度
,无人机的飞行高度![]() 米,桥的长度
米,桥的长度![]() 为1255米.
为1255米.
(1)求点![]() 到桥左端点
到桥左端点![]() 的距离;
的距离;
(2)若从无人机前端点![]() 测得正前方的桥的右端点
测得正前方的桥的右端点![]() 的俯角为
的俯角为![]() ,求这架无人机的长度
,求这架无人机的长度![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com