
【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()
【答案】(1)x=11,y=2,m=0.22;(2)C等扇形的圆心角的度数为43.2度;(3)这700名学生中成绩达到A等和B等的人数共有574人.
【解析】
(1)根据扇形统计图求出A等的人数,再减去得10分的人数即可求出x值与频率m值,再用总人数减去各分值人数求出y值;(2)先求出n的值,再求出C组的占比,即可求出其圆心角度数;(3)根据A组,B组的频率即可估计这700名学生中成绩达到A等和B等的人数.
(1)x=50×36%﹣7=11,
y=50-(7+11+15+8+4+3)=2,
m=11÷50=0.22;
(2)∵n=2÷50=0.04,
∴C等扇形的圆心角的度数为:(0. 08+0.04)×360°=43.2度;
(3)达到A等和B等的人数为:(0.14+0.22+0.3+0.16)×700=574人.
答:这700名学生中成绩达到A等和B等的人数共有574人.


科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
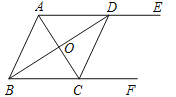
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生会为了考察该校1800名学生参加课外体育活动的情况,采取抽样调查的方法从“篮球、排球、乒乓球、足球及其他”等五个方面调查了若干名学生的兴趣爱好(每人只能选其中一项),并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息,下列判断:①本次抽样调查的样本容量是60;②在扇形统计图中,“其他”部分所对应的圆心角是60°;③该校学生中喜欢“乒乓球”的人数约为450人;④若被抽查的男女学生数相同,其中喜欢球类的男生占喜欢球类人数的56.25%,则被抽查的学生中,喜欢“其他”类的女生数为9人.其中正确的判断是( )

A. 只有①②③B. 只有①②④C. 只有①③④D. 只有③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点A,B,C,D分别在l1,l2,l3,l4上,过点D作DE⊥l1于点E,已知相邻两条平行线之间的距离为1,求AE及正方形ABCD的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,随着我国的科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,一般的高铁包括G字头的高速动车组以及D字头的动车组.由大连到北京的G377的平均速度是D31的平均速度的1.2倍,行驶相同的路程1500千米,G377少用1个小时.
(1)求D31的平均速度.
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式.现阶段D31票价为266元/张,G377票价为400元/张,如果你有机会给有关部门提一个合理化建议,使G377的性价比达到D31的性价比,你如何建议,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我镇绿色和特色农产品在市场上颇具竞争力.外贸商胡经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如图)帮胡经理解决以下问题:
(1)若胡经理想将这批蘑菇存放x天后一次性出售, 则x天后这批蘑菇的销售单价为元, 这批蘑菇的销售量是千克;
(2)胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量).
(3)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.
现有点A(2,0)和抛物线E上的点B(-1,n),请完成下列任务: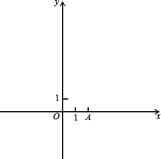
(1)【尝试】
①当t=2时,抛物线E的顶点坐标是.
②点A抛物线E上;(填“在”或“不在”),
③n=.
(2)【发现】通过②和③的演算可知,对于t取任何不为零的实数,抛物线E总过定点,这个定点的坐标是.
(3)【应用1】二次函数y=-3x2+5x+2是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
(4)【应用2】以AB为一边作矩形ABCD,使得其中一个顶点落在y轴上,若抛物线E经过点A、B、C,求出所有符合条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.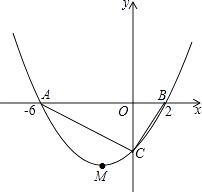
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com