
【题目】如图所示,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.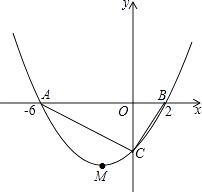
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
【答案】
(1)解:设此函数的解析式为y=a(x+h)2+k,
∵函数图象顶点为M(﹣2,﹣4),
∴y=a(x+2)2﹣4,
又∵函数图象经过点A(﹣6,0),
∴0=a(﹣6+2)2﹣4
解得a= ![]() ,
,
∴此函数的解析式为y= ![]() (x+2)2﹣4,即y=
(x+2)2﹣4,即y= ![]() x2+x﹣3
x2+x﹣3
(2)解:∵点C是函数y= ![]() x2+x﹣3的图象与y轴的交点,
x2+x﹣3的图象与y轴的交点,
∴点C的坐标是(0,﹣3),
又当y=0时,有y= ![]() x2+x﹣3=0,
x2+x﹣3=0,
解得x1=﹣6,x2=2,
∴点B的坐标是(2,0),
则S△ABC= ![]() |AB||OC|=
|AB||OC|= ![]() ×8×3=12
×8×3=12
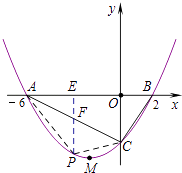
(3)解:假设存在这样的点,过点P作PE⊥x轴于点E,交AC于点F.
设E(x,0),则P(x, ![]() x2+x﹣3),
x2+x﹣3),
设直线AC的解析式为y=kx+b,
∵直线AC过点A(﹣6,0),C(0,﹣3),
∴ ![]() ,
,
解得  ,
,
∴直线AC的解析式为y=﹣ ![]() x﹣3,
x﹣3,
∴点F的坐标为F(x,﹣ ![]() x﹣3),
x﹣3),
则|PF|=﹣ ![]() x﹣3﹣(
x﹣3﹣( ![]() x2+x﹣3)=﹣
x2+x﹣3)=﹣ ![]() x2﹣
x2﹣ ![]() x,
x,
∴S△APC=S△APF+S△CPF
= ![]() |PF||AE|+
|PF||AE|+ ![]() |PF||OE|
|PF||OE|
= ![]() |PF||OA|=
|PF||OA|= ![]() (﹣
(﹣ ![]() x2﹣
x2﹣ ![]() x)×6=﹣
x)×6=﹣ ![]() x2﹣
x2﹣ ![]() x=﹣
x=﹣ ![]() (x+3)2+
(x+3)2+ ![]() ,
,
∴当x=﹣3时,S△APC有最大值 ![]() ,
,
此时点P的坐标是P(﹣3,﹣ ![]() )
)
【解析】(1)根据顶点坐标公式即可求得a、b、c的值,即可解题;(2)易求得点B、C的坐标,即可求得OC的长,即可求得△ABC的面积,即可解题;(3)作PE⊥x轴于点E,交AC于点F,可将△APC的面积转化为△AFP和△CFP的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示△APC的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
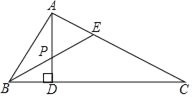
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,有阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式 (用字母表示)
(应用)请应用这个公式完成下列各题
①已知![]() ,
,![]() ,则
,则![]() 的值为
的值为
②计算:![]()
(拓展)①![]() 结果的个位数字为
结果的个位数字为
②计算:![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“让世界充满爱”的捐款助学活动,其中八(2)班全体同学的捐款情况如下表:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 12 | 3 |
由于填表的同学不小心把墨水滴在了表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的36%,结合上表回答下列问题:
(1)八(2)班共有多少人?
(2)学生捐款金额的众数和中位数分别为多少元?
(3)如果把该班学生的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对应的扇形圆心角为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 分别在线段
分别在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() 平分
平分![]() .
.
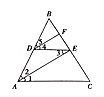
(1)求证:![]() 平分
平分![]() 阅读下列推理过程,并将推理过程补充完整.
阅读下列推理过程,并将推理过程补充完整.
证明:![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ( )
( )
故 .(等量代换)
![]() ,(已知)
,(已知)
![]() ,( )
,( )
![]() ,( )
,( )
![]() ,
,
![]() 平分
平分![]() .( )
.( )
(2)若![]() ,请直接写出图中所有与
,请直接写出图中所有与![]() 互余的角.
互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现规定:求若千个相同的有理数(均不等于![]() )的商的运算叫做除方,比如
)的商的运算叫做除方,比如![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,
次方”,![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,一般地,把
次方”,一般地,把![]() 个
个![]()
![]() 相除记作
相除记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”.
次方”.
初步探究:(1)直接写出结果:![]() .
.![]() .
.
(2)下列关于除方的说法中,错误的是
A.任何非零数的圈![]() 次方都等于
次方都等于![]()
B.对于任何正整数![]() 的圈
的圈![]() 次方等于
次方等于![]()
C.![]()
D.负数的圈奇数次方的结果是负数,负数的圈偶数次方的结果是正数
深入思考:我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(3)试一试,把下列除方运算直接写成幂的形式![]() .
. .
.
(4)想一想,请把有理数![]() 的圈
的圈![]() 次方写成幂的形式.
次方写成幂的形式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x﹣y=7;②4x+1=x﹣y;③![]() +y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
+y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=﹣ ![]() x+8,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP,连结PQ,设点P的坐标为P(0,t).
x+8,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP,连结PQ,设点P的坐标为P(0,t).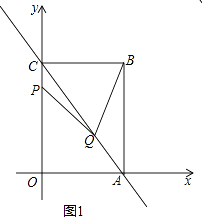
(1)求点B的坐标.
(2)若t=1时,连接BQ,求△ABQ的面积.
(3)如图2,以PQ为直径作⊙I,记⊙I与射线AC的另一个交点为E.
①若 ![]() =
= ![]() ,求此时t的值.
,求此时t的值.
②若圆心I在△ABC内部(不包含边上),则此时t的取值范围为是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com