
【题目】如图,已知点![]() 分别在线段
分别在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() 平分
平分![]() .
.
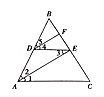
(1)求证:![]() 平分
平分![]() 阅读下列推理过程,并将推理过程补充完整.
阅读下列推理过程,并将推理过程补充完整.
证明:![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ( )
( )
故 .(等量代换)
![]() ,(已知)
,(已知)
![]() ,( )
,( )
![]() ,( )
,( )
![]() ,
,
![]() 平分
平分![]() .( )
.( )
(2)若![]() ,请直接写出图中所有与
,请直接写出图中所有与![]() 互余的角.
互余的角.
【答案】(1)![]() ;两直线平行,内错角相等;
;两直线平行,内错角相等;![]() ;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;(2)
;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;(2)![]() 和
和![]()
【解析】
(1)根据角平分线的定义得到∠1=∠2,根据平行线的性质得到∠1=∠3,等量代换得到∠2=∠3,根据平行线的性质得到∠2=∠5,等量代换即可得到结论;
(2)根据垂直的定义得到∠3+∠DEB=90°,∠1+∠C=90°,由平行线的性质得出∠5+∠B=90°,然后由∠3=∠1=∠4=∠5得出与∠1互余的角.
解:(1)![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ,(两直线平行,内错角相等)
,(两直线平行,内错角相等)
故![]() (等量代换)
(等量代换)
![]() ,(已知)
,(已知)
![]() ,(两直线平行,同位角相等)
,(两直线平行,同位角相等)
![]() ,(两直线平行,内错角相等)
,(两直线平行,内错角相等)
![]() ,(等量代换)
,(等量代换)
![]() 平分
平分![]() .(角平分线的定义)
.(角平分线的定义)
故答案为:![]() ;两直线平行,内错角相等;
;两直线平行,内错角相等;![]() ;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;
;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;
(2)∵![]() ,
,![]()
∴∠AEB=∠DFB=90°
∴∠3+∠DEB=90°,∠1+∠C=90°,∠5+∠B=90°,
又由①可知∠3=∠1=∠4=∠5
∴∠1+∠DEB=90°,∠1+∠B=90°,
∴与![]() 互余的角有
互余的角有![]() 和
和![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】近年来,随着我国的科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,一般的高铁包括G字头的高速动车组以及D字头的动车组.由大连到北京的G377的平均速度是D31的平均速度的1.2倍,行驶相同的路程1500千米,G377少用1个小时.
(1)求D31的平均速度.
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式.现阶段D31票价为266元/张,G377票价为400元/张,如果你有机会给有关部门提一个合理化建议,使G377的性价比达到D31的性价比,你如何建议,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式![]() 计算出每一行的数据.第一行表示年级,第二行表示班级,第三行表示班级学号的十位数,第四行表示班级学号的个位数.如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的统一学号为_______.
计算出每一行的数据.第一行表示年级,第二行表示班级,第三行表示班级学号的十位数,第四行表示班级学号的个位数.如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的统一学号为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.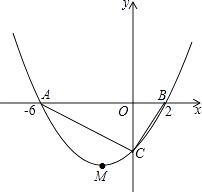
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的是( )

A. AE=BE B. DE⊥CE C. CD=AD+BC D. CD=AD+CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从![]() 地前往
地前往![]() 地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.
地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.
(1)求![]() ,
,![]() 两地的路程是多少千米?
两地的路程是多少千米?
(2)当甲到达![]() 地后,乙再与甲同时从
地后,乙再与甲同时从![]() 地按各自的原速返回
地按各自的原速返回![]() 地,若他们由
地,若他们由![]() 地返回
地返回![]() 地的过程中所行走路程的和为180千米,则甲走了多少小时?
地的过程中所行走路程的和为180千米,则甲走了多少小时?
(3)若乙到达![]() 地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米?
地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
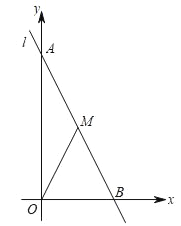
【题目】如图,已知在平面直角坐标中,直线l:y=﹣2x+6分别交两坐标于A、B两点,M是级段AB上一个动点,设点M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)当△OMB的面积是△OAB面积的![]() 时,求点M的坐标;
时,求点M的坐标;
(3)当△OMB是以OB为底的等腰三角形,求它的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com