
【题目】已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 轴相交于点
轴相交于点![]() ,抛物线与
,抛物线与![]() 轴相交于点
轴相交于点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;

(3)如图2,点![]() 是折线
是折线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,直线
轴,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 落在
落在![]() 轴上,请直接写出
轴上,请直接写出![]() 点的坐标.
点的坐标.

【答案】(1) 抛物线的解析式为![]() ;(2)
;(2)![]() 的面积为
的面积为![]() 或
或![]() ;(3)Q点坐标为:(-
;(3)Q点坐标为:(-![]() ,
,![]() )或
)或![]() 或
或![]() .
.
【解析】(1)把点![]() 代入
代入![]() ,求得
,求得![]() 的值即可得;
的值即可得;
(2)由已知可求得直线![]() 的解析式为:
的解析式为:![]() ,根据解析式易求
,根据解析式易求![]() ,由
,由![]() ,继而可求得
,继而可求得![]() 的长,设点
的长,设点![]() ,可得关于t的方程,解方程求得t的值,根据对称性可知方程的解都满足条件,由此即可得;
,可得关于t的方程,解方程求得t的值,根据对称性可知方程的解都满足条件,由此即可得;
(3)若分点Q在AB要,点Q在BC上,且Q在y轴左侧, Q在BC上,且Q在y轴右侧,三种情况分别讨论即可得.
(1)把点![]() 代入
代入![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ,
,
即![]() ;
;
(2)由(1)可得点A的坐标为(![]() ,-2).
,-2).
设直线![]() 解析式为:
解析式为:![]() ,代入点
,代入点![]() 的坐标得:
的坐标得:
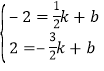 ,解得:
,解得:![]() ,∴直线
,∴直线![]() 的解析式为:
的解析式为:![]() ,
,
易求得![]() ,
,
若![]() ,
,
当![]() 时,则有
时,则有![]() ,
,
![]() ,
,
设点![]() ,则:
,则:![]() ,
,
解得![]() ,
,![]() ,
,
由对称性知;当![]() 时,也满足
时,也满足![]() ,
,
![]() ,
,![]() 都满足条件,
都满足条件,
![]() 的面积
的面积![]() ,
,![]() 的面积为
的面积为![]() 或
或![]() ;
;
(3)若Q在AB上运动,如图:设Q(a,-2a-1),则QN=-2a,NE=-a,QN1=-2a,
易知△QRN1∽△N1SE,
∴![]() ,
,
a=-![]() ,∴Q(-
,∴Q(-![]() ,
,![]() );
);
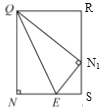
若Q在BC上运动,且Q在y轴左侧,如图:设NE=a,则N1E=a,
易知RN1=2,SN1=1,QN1=QN=3,
∴QR=![]() ,SE=
,SE=![]() ,
,
Rt△SEN1中,![]() ,
,
![]() ,∴Q
,∴Q![]() ;
;

若Q在BC上运动,且Q在y轴右侧,如图:设NE=a,则N1E=a,
易知RN1=2,SN1=1,QN1=QN=3,
∴QR=![]() ,SE=
,SE=![]() ,
,
Rt△SEN1中,![]() ,
,
![]() ,∴Q
,∴Q![]() ;
;
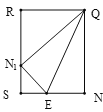
综上所述Q点坐标为:(-![]() ,
,![]() )或
)或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=-2x+5
(1)画出它的图像
(2)求当x=2时,y的值
(3)求当y=-3时,x的值
(4)观察图像,直接写出当x为何值时,y>0,y=0,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读短文,解决问题
如果一个三角形和一个菱形满足条件:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”.如图1,菱形AEFD为△ABC的“亲密菱形”.
如图2,在△ABC中,以点A为圆心,以任意长为半径作弧,交AB、AC于点M、N,再分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
(1)求证:四边形AEFD是△ABC的“亲密菱形”;
(2)当AB=6,AC=12,∠BAC=45°时,求菱形AEFD的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AM∥BN,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA,NB分别相交于点D,E.
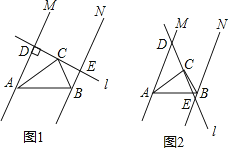
(1)如图1,当直线l与直线MA垂直时,试探究AB,AD,BE之间的数量关系并说明理由;
(2)如图2,当直线l与直线MA不垂直,且交点D,E在AB的异侧时,则(1)的结论还成立吗?若成立,请说明理由;若不成立,请直接写出AB,AD,BE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
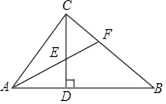
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了建设社会主义新农村,我市积极推进“行政村通畅工程”.A村和B村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的关系的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
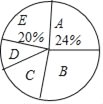
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com