
【题目】阅读短文,解决问题
如果一个三角形和一个菱形满足条件:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”.如图1,菱形AEFD为△ABC的“亲密菱形”.
如图2,在△ABC中,以点A为圆心,以任意长为半径作弧,交AB、AC于点M、N,再分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
(1)求证:四边形AEFD是△ABC的“亲密菱形”;
(2)当AB=6,AC=12,∠BAC=45°时,求菱形AEFD的面积.


【答案】(1)证明见解析;(2) 四边形![]() 的面积为
的面积为![]() .
.
【解析】(1)根据尺规作图可知AF平分∠BAC,再根据DF//AC,可得AD=DF,再由两组对边分别平行的四边形是平行四边形可得四边形AEFD是平行四边形,继而可得平行四边形AEFD是菱形,根据“亲密菱形”的定义即可得证;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,可证得△BDF∽△BAC,根据相似三角形的性质可求得a=4,过D作DG⊥AC,垂足为G,在Rt△ADG中, DG=2![]() ,继而可求得面积.
,继而可求得面积.
(1)由尺规作图可知AF平分∠BAC,
∴∠DAF=∠EAF,
∵DF//AC,∴∠DFA=∠EAF,∴∠DAF=∠DFA,∴AD=DF,
∵FD//AC,FE//AB,∴四边形AEFD是平行四边形,
∴平行四边形AEFD是菱形,
∵∠BAC与∠DAE重合,点F点BC上,
∴菱形AEFD为△ABC的“亲密菱形”;
(2)设菱形的边长为a,即DF=AD=a,则BD=6-a,
∵DF//AC,∴△BDF∽△BAC,
∴BD:BA=BF:AC,
即(6-a):6=a:12,
∴a=4,
过D作DG⊥AC,垂足为G,
在Rt△ADG中,∠DAG=45°,∴DG=![]() AD=2
AD=2![]() ,
,
∴S菱形AEFD=AEDG=8![]() ,
,
即四边形AEFD的面积为8![]() .
.



 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
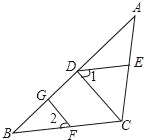
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,若一弹簧长度(cm)与所挂物体质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
则下列说法错误的是( )
A.弹簧长度随物体的质量的变化而变化,物体的质量是自变量,弹簧的长度是因变量
B.如果物体的质量为x kg,那么弹簧的长度y cm可以表示为y=12+0.5x
C.在弹簧能承受的范围内,当物体的质量为7kg时,弹簧的长度为16cm
D.在没挂物体时,弹簧的长度为12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率估计概率的实验中,统计了某一个结果出现的频率,绘制了如下的表格,则符合这一结果的实验可能是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1200 |
频率 | 0.430 | 0.360 | 0.320 | 0.328 | 0.330 | 0.329 |
A. 抛一枚质地均匀的硬币,出现正面的概率
B. 从一个装有3个红球和2个白球的不透明袋子里任取1球,取出红球的概率
C. 掷一枚均匀的正方体骰子,出现的点数是3的倍数的概率
D. 从正方形、正五边形、正六边形中任意取一个图形,是轴对称图形的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全市中学运动会800m比赛中,甲、乙两名运动员同时起跑,刚跑出200m后,甲不慎摔倒,他又迅速地爬起来继续投入比赛,并取得了优异的成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系,根据图象解答下列问题:

(1)甲再次投入比赛后,甲的速度为;
(2)甲再次投入比赛后,在距离终点多远处追上乙?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 轴相交于点
轴相交于点![]() ,抛物线与
,抛物线与![]() 轴相交于点
轴相交于点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;

(3)如图2,点![]() 是折线
是折线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,直线
轴,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 落在
落在![]() 轴上,请直接写出
轴上,请直接写出![]() 点的坐标.
点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com