
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

【答案】(1)![]() ;(2)x>1;(3)P(﹣
;(2)x>1;(3)P(﹣![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)求得A(1,3),把A(1,3)代入双曲线y=![]() ,可得y与x之间的函数关系式;
,可得y与x之间的函数关系式;
(2)依据A(1,3),可得当x>0时,不等式![]() x+b>
x+b>![]() 的解集为x>1;
的解集为x>1;
(3)分两种情况进行讨论,AP把△ABC的面积分成1:3两部分,则CP=![]() BC=
BC=![]() ,或BP=
,或BP=![]() BC=
BC=![]() ,即可得到OP=3﹣
,即可得到OP=3﹣![]() =
=![]() ,或OP=4﹣
,或OP=4﹣![]() =
=![]() ,进而得出点P的坐标.
,进而得出点P的坐标.
(1)把A(1,m)代入y1=﹣x+4,可得m=﹣1+4=3,
∴A(1,3),
把A(1,3)代入双曲线y=![]() ,可得k=1×3=3,
,可得k=1×3=3,
∴y与x之间的函数关系式为:y=![]() ;
;
(2)∵A(1,3),
∴当x>0时,不等式![]() x+b>
x+b>![]() 的解集为:x>1;
的解集为:x>1;
(3)y1=﹣x+4,令y=0,则x=4,
∴点B的坐标为(4,0),
把A(1,3)代入y2=![]() x+b,可得3=
x+b,可得3=![]() +b,
+b,
∴b=![]() ,
,
∴y2=![]() x+
x+![]() ,
,
令y2=0,则x=﹣3,即C(﹣3,0),
∴BC=7,
∵AP把△ABC的面积分成1:3两部分,
∴CP=![]() BC=
BC=![]() ,或BP=
,或BP=![]() BC=
BC=![]()
∴OP=3﹣![]() =
=![]() ,或OP=4﹣
,或OP=4﹣![]() =
=![]() ,
,
∴P(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
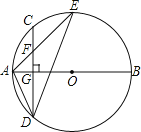
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系中.
在平面直角坐标系中.

(1)写出![]() 、
、![]() 、
、![]() 三点的坐标:
三点的坐标:
![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)![]() 的面积为_______.
的面积为_______.
(3)联结![]() ,在平面直角坐标系中找一个点
,在平面直角坐标系中找一个点![]() ,使
,使![]() 为等腰直角三角形,且以
为等腰直角三角形,且以![]() 为直角边,则
为直角边,则![]() 的坐标是________(直接写答案).
的坐标是________(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-6,0),B(-1,1),C(-3,3),将△ABC绕点B按顺时针方向旋转90°后得到△A1BC1.
(1)画出△A1BC1,写出点A1、C1的坐标;
(2)计算线段BA扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市高中招生体育考试前教育部门为了解全市九年级男生考试项目的选择情况(每人限选一项),对全市部分九年级男生进行了调查,将调查结果分成五类:A、实心球(2kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)将上面的条形统计图补充完整;
(2)假定全市九年级毕业学生中有5500名男生,试估计全市九年级男生中选“50米跑”的人数有多少人?
(3)甲、乙两名九年级男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球和立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,点E、F分别在CD、AD上,CE=DF,BE、CF相交于点G,若图中阴影部分的面积与正方形ABCD的面积之比为3:4,则△BCG的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知 RtABC 中,![]() ,一条直角边为1,如果RtABC 是“有趣三角形”,那么这个三角形“有趣中线”的长等于_____
,一条直角边为1,如果RtABC 是“有趣三角形”,那么这个三角形“有趣中线”的长等于_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com