
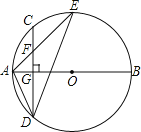
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=![]() .
.
【答案】①证明见解析;
②2;
③证明见解析.
【解析】试题分析:(1)由垂径定理可得弧AC=弧AD,根据等弧所对的圆周角相等,可得∠ADF=∠AED,,根据两角对应相等的两个三角形相似的判定定理,即可证得△ADF∽△AED;
(2)根据![]() =
=![]() ,CF=2,可得FD=6,故可得CD的长,根据垂径定理即可求得CG的长,再根据CG-CF即可得FG的长。
,CF=2,可得FD=6,故可得CD的长,根据垂径定理即可求得CG的长,再根据CG-CF即可得FG的长。
(3)在Rt△AGF中由勾股定理求得AG的长,根据垂径定理和同弧所对的圆周角相等的性质,可知∠E=∠ADF,再根据三角函数定义即可证得tanE的值.
解:①∵AB是⊙O的直径,弦CD⊥AB,
∴DG=CG,
∴弧AD=弧AC,∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
②∵![]() =
=![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG﹣CF=2;
③∵AF=3,FG=2,∴AG=![]() ,
,
tan∠E=![]() .
.


科目:初中数学 来源: 题型:
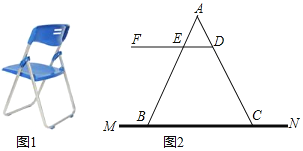
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图![]() 图
图![]() ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得![]() 厘米,
厘米, ![]() 厘米,
厘米, ![]() .
.
![]() 求椅子的高度
求椅子的高度![]() 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离![]() 精确到1厘米
精确到1厘米![]()
![]() 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离![]() 精确到1厘米
精确到1厘米![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表:
输入汉字个数(个) | 132 | 133 | 134 | 135 | 136 | 137 | ||
甲班人数人) | 1 | 0 | 2 | 4 | 1 | 2 | ||
乙班人数(人) | 0 | 1 | 4 | 1 | 2 | 2 | ||
请分别判断下列同学是说法是否正确,并说明理由.
(1)两个班级输入汉字个数的平均数相同;
(2)两个班学生输入汉字的中位数相同众数也相同;
(3)甲班学生比乙班学生的成绩稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①内错角相等;②对顶角相等;③三角形的一个外角大于任何一个内角;④若三条线段![]() 、
、![]() 、
、![]() 满足
满足![]() ,则三条线段
,则三条线段![]() 、
、![]() 、
、![]() 一定能组成三角形其中正确的个数是( )
一定能组成三角形其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 (1)所示,圆内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.
(1)求证阴影部分四边形OFCG的面积是△ABC面积的![]() ;
;
(2)如图 (2)所示,若∠DOE保持120°角度不变,求证当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接线下开学,某学校决定对原有的排水系统进行改造,如果甲组先做5天后,剩下的工程由乙组单独承担,还需7.5天才能完工,为了早日完成工程,甲乙两组合作施工,6天完成了任务;甲乙两组单独完成此项工程各需要多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com