
【题目】如图 (1)所示,圆内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.
(1)求证阴影部分四边形OFCG的面积是△ABC面积的![]() ;
;
(2)如图 (2)所示,若∠DOE保持120°角度不变,求证当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)本题要依靠辅助线的帮助.连接OA,OC,证明Rt△OFC≌Rt△OGC≌Rt△OGA后求得S△OAC=![]() SΔABC,易证SOFCG=
SΔABC,易证SOFCG=![]() SΔABC.
SΔABC.
(2)本题有多种解法.连接OA,OB和OC,证明△AOC≌△COB≌△BOA,求出∠AOC以及∠DOE之间的关系即可.
解:(1)连接OA,OC,∵点O是等边三角形ABC的外心,Rt△OFC≌Rt△OGC≌Rt△OGA,S四边形OFCG=2S△OFC=S△OAC.∵S△OAC=![]() S△ABC,∴S四边形OFCG=
S△ABC,∴S四边形OFCG=![]() S△ABC.
S△ABC.
(2)证法1:如图 (1)所示,连接OA,OB和OC,则△AOC≌△COB≌△BOA,∠1=∠2.不妨设OD交BC于点F,OE交AC于点G,∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,∴∠3=∠5.在△OAG和△OCF中,  ∴△OAG≌△OCF,∴S四边形OFCG=S△AOC=
∴△OAG≌△OCF,∴S四边形OFCG=S△AOC=![]() S△ABC.证法2:如图 (2)所示,不妨设OD交BC于点F,OE交AC于点G,作DH⊥BC,OK⊥AC,垂足分别为点H,K.在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360°-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四边形OFCG=S四边形OHCK=
S△ABC.证法2:如图 (2)所示,不妨设OD交BC于点F,OE交AC于点G,作DH⊥BC,OK⊥AC,垂足分别为点H,K.在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360°-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四边形OFCG=S四边形OHCK=![]() S△ABC.
S△ABC.



科目:初中数学 来源: 题型:
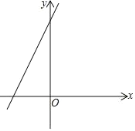
【题目】如图,直线l:y=2x+4
(1)①直接写出直线l关于y轴对称的直线l1的解析式_______.
②直接写出直线l向右平移2个单位得到的直线l2的解析式________.
(2)在(1)的基础上,点M是x轴上一点,过点M作x轴的垂线交直线l1于点Q、交直线l2于点P.若PM=2PQ,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60![]() 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120![]() 海里。
海里。

(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.45)
=2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】底边长为6厘米,高为9厘米的等腰三角形20个,迭放如图:
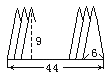
每两个等腰三角形有等距离的间隔,底边迭合在一起的长度是44厘米.回答下列问题:
(1)两个三角形的间隔距离;
(2)三个三角形重迭(两次)部分的面积之和;
(3)只有两个三角形重迭(一次)部分的面积之和;
(4)迭到一起的总面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
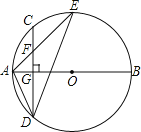
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系中.
在平面直角坐标系中.

(1)写出![]() 、
、![]() 、
、![]() 三点的坐标:
三点的坐标:
![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)![]() 的面积为_______.
的面积为_______.
(3)联结![]() ,在平面直角坐标系中找一个点
,在平面直角坐标系中找一个点![]() ,使
,使![]() 为等腰直角三角形,且以
为等腰直角三角形,且以![]() 为直角边,则
为直角边,则![]() 的坐标是________(直接写答案).
的坐标是________(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市高中招生体育考试前教育部门为了解全市九年级男生考试项目的选择情况(每人限选一项),对全市部分九年级男生进行了调查,将调查结果分成五类:A、实心球(2kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)将上面的条形统计图补充完整;
(2)假定全市九年级毕业学生中有5500名男生,试估计全市九年级男生中选“50米跑”的人数有多少人?
(3)甲、乙两名九年级男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球和立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暖羊羊有5张写着不同数字的卡片,请你按要求选择卡片,完成下列各问题:
![]()
(1)从中选择两张卡片,使这两张卡片上数字的乘积最大.
这两张卡片上的数字分别是 ,积为 _.
(2)从中选择两张卡片,使这两张卡片上数字相除的商最小.
这两张卡片上的数字分别是 ,商为 .
(3)从中选择4张卡片,每张卡片上的数字只能用一次,选择加、减、乘、除中的适当方法(可加括号),使其运算结果为24,写出运算式子.(写出一种即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com