
【题目】如图,直线l:y=2x+4
(1)①直接写出直线l关于y轴对称的直线l1的解析式_______.
②直接写出直线l向右平移2个单位得到的直线l2的解析式________.
(2)在(1)的基础上,点M是x轴上一点,过点M作x轴的垂线交直线l1于点Q、交直线l2于点P.若PM=2PQ,求M点的坐标.
【答案】(1)①y=﹣2x+4;②y=2x;(2)M(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)①先求出点A,B坐标,再利用对称性求出点C坐标,最后利用待定系数法即可得出结论;
②利用平移的性质即可得出结论;
(2)设出点M坐标,进而表示出点P,Q坐标,即可表示出PM,PQ,最后建立方程求解即可得出结论.
解:①如图,记直线y=2x+4与y轴的交点为A,与x轴的交点为B,
∴A(﹣2,0),B(0,4),
∴点A关于y轴的对称点C的坐标为(2,0),
设直线l1的解析式的解析式为y=kx+4,
∴2k+4=0,
∴k=﹣2,
∴直线l1的解析式y=﹣2x+4;
②直线l:y=2x+4向右平移2个单位得到的直线l2的解析式y=2(x﹣2)+4=2x,
故答案为:y=﹣2x+4,y=2x;
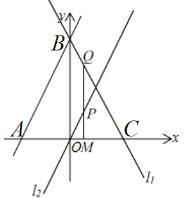
(2)如图,
设点M(m,0),
∵点P在直线l2:y=2x上,
∴P(m,2m),
∵点Q在直线l1:y=﹣2x+4上,
∴Q(m,﹣2m+4),
∴PM=|2m|,PQ=|2m﹣(﹣2m+4)|=4|m﹣1|,
∵PM=2PQ,
∴|2m|=2×4|m﹣1|,
∴m=![]() 或m=
或m=![]() ,
,
∴M(![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
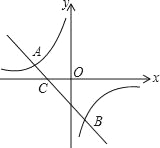
【题目】如图,已知A(﹣4,2),B(n,﹣4)是一次函数y=kx+b的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象写出使一次函数的函数值小于反比例函数的函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位自然数是![]() ,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数
,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数![]() (
(![]() 可以与
可以与![]() 相同),设
相同),设![]() ,在
,在![]() 所有的可能情况中,当
所有的可能情况中,当![]() 最大时,我们称此时的
最大时,我们称此时的![]() 是
是![]() 的“梦想数”,并规定
的“梦想数”,并规定![]() .例如127按上述方法可得到新数有:217、172、721,因为
.例如127按上述方法可得到新数有:217、172、721,因为![]() 所以172是172的“梦想数”,此时,
所以172是172的“梦想数”,此时,![]() .
.
(1)求512的“梦想数”及![]() 的值;
的值;
(2)设三位自然数![]() 交换其个位与十位上的数字得到新数
交换其个位与十位上的数字得到新数![]() ,若
,若![]() ,且
,且![]() 能被7整除,求
能被7整除,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
问:(1)这个小组男生的达标率为多少?(达标率=![]() )
)
(2)这个小组男生的平均成绩是多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
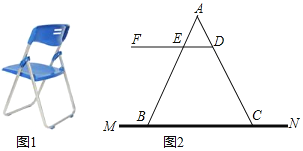
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图![]() 图
图![]() ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得![]() 厘米,
厘米, ![]() 厘米,
厘米, ![]() .
.
![]() 求椅子的高度
求椅子的高度![]() 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离![]() 精确到1厘米
精确到1厘米![]()
![]() 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离![]() 精确到1厘米
精确到1厘米![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为 ______
DM=BD+BE=4cm+4cm=8cm,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 (1)所示,圆内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.
(1)求证阴影部分四边形OFCG的面积是△ABC面积的![]() ;
;
(2)如图 (2)所示,若∠DOE保持120°角度不变,求证当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com