【题目】底边长为6厘米，高为9厘米的等腰三角形20个，迭放如图：

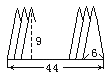
每两个等腰三角形有等距离的间隔，底边迭合在一起的长度是44厘米．回答下列问题：

（1）两个三角形的间隔距离；

（2）三个三角形重迭（两次）部分的面积之和；

（3）只有两个三角形重迭（一次）部分的面积之和；

（4）迭到一起的总面积．

参考答案：

【答案】（1）两个三角形的间隔距离为2厘米；

（2）三个三角形重迭（两次）部分的面积之和为54平方厘米；

（3）只有两个三角形重迭（一次）部分的面积之和为120平方厘米；

（4）迭到一起的总面积为312平方厘米．

【解析】

（1）因为20个三角形迭放，有（20-1）个间隔，用（44-6）÷（20-1）就是要求的答案；
（2）因为每三个连着的三角形重迭产生这样的一个符合条件的小三角形，每增加一个大三角形，就多产生一个三次重迭的三角形，而且与前一个不重迭，因此这样的小三角形共有（20-2）个，三次重迭的三角形的底是原来三角形底的，高是原来三角形高的，由此即可解答；
（3）每两个连着的三角形重迭部分，也是原来的三角形一般模样的三角形，每增加一个大三角形，就产生一个小三角形，共产生（20-1）个，由此符合条件面积即可求出；
（4）20个三角形的面积之和减去重迭部分，其中120平方厘米重迭一次，54平方厘米重迭两次，由此问题即可解决．

解：（1）（44﹣6）÷（20﹣1）＝2（厘米），

（2）6××9×××（20﹣2），

＝3×18，

＝54（平方厘米）；

（3）（6××9××）×（20﹣1）﹣54×2，

＝12×19﹣108，

＝228﹣108，

＝120（平方厘米）；

（4）6×9××20﹣120﹣54×2，

＝540﹣120﹣108，

＝420﹣108，

＝312（平方厘米），

答：（1）两个三角形的间隔距离是2厘米；

（2）三个三角形重迭（两次）部分的面积之和是54平方厘米；

（3）只有两个三角形重迭（一次）部分的面积之和是120平方厘米；

（4）迭到一起的总面积是312平方厘米．

关闭