
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bxЉ2гыxжсНЛгкЕуAЁЂBЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌЉ2ЃЉЃЌOB=4OAЃЌtanЁЯBCO=2ЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЕуMЁЂNЗжБ№ЪЧЯпЖЮBCЁЂABЩЯЕФЖЏЕуЃЌЕуMДгЕуBГіЗЂвдУПУы![]() ИіЕЅЮЛЕФЫйЖШЯђЕуCдЫЖЏЃЌЭЌЪБЕуNДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛЕФЫйЖШЯђЕуBдЫЖЏЃЌЕБЕуMЁЂNжаЕФвЛЕуЕНДяжеЕуЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЙ§ЕуMзїMPЁЭxжсгкЕуEЃЌНЛХзЮяЯпгкЕуPЃЎЩшЕуMЁЂЕуNЕФдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌЕБtЮЊЖрЩйЪБЃЌЁїPNEЪЧЕШбќШ§НЧаЮЃП
ИіЕЅЮЛЕФЫйЖШЯђЕуCдЫЖЏЃЌЭЌЪБЕуNДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛЕФЫйЖШЯђЕуBдЫЖЏЃЌЕБЕуMЁЂNжаЕФвЛЕуЕНДяжеЕуЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЙ§ЕуMзїMPЁЭxжсгкЕуEЃЌНЛХзЮяЯпгкЕуPЃЎЩшЕуMЁЂЕуNЕФдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌЕБtЮЊЖрЩйЪБЃЌЁїPNEЪЧЕШбќШ§НЧаЮЃП

ЁОД№АИЁПЃЈ1ЃЉAЃЈЉ1ЃЌ0ЃЉЃЛЃЈ2ЃЉy=![]() x2Љ
x2Љ![]() xЉ2ЃЛЃЈ3ЃЉЕБt=1ЪБЃЌЁїPNEЪЧЕШбќШ§НЧаЮЃЎ
xЉ2ЃЛЃЈ3ЃЉЕБt=1ЪБЃЌЁїPNEЪЧЕШбќШ§НЧаЮЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩCЃЈ0ЃЌЉ2ЃЉжЊOC=2ЃЌИљОнtanЁЯBCO=![]() =2ЕУOB=4ЃЌОнДЫЕУГіЕуBзјБъЃЌдйгЩOB=4OAПЩЕУЕуAзјБъЃЛ
=2ЕУOB=4ЃЌОнДЫЕУГіЕуBзјБъЃЌдйгЩOB=4OAПЩЕУЕуAзјБъЃЛ
ЃЈ2ЃЉНЋЕуAЁЂBзјБъДњШыХзЮяЯпНтЮіЪНЧѓЕУaЁЂbЕФжЕЃЌДгЖјЕУГіД№АИЃЛ
ЃЈ3ЃЉгЩЬтвтжЊAN=2tЁЂBM=![]() tЃЌИљОнtanЁЯBME=tanЁЯBCO=2жЊ
tЃЌИљОнtanЁЯBME=tanЁЯBCO=2жЊ![]() =
=![]() ЃЌЧѓЕУOE=OBЉBE=4ЉtЃЌДгЖјЕУГіPE=Љ
ЃЌЧѓЕУOE=OBЉBE=4ЉtЃЌДгЖјЕУГіPE=Љ![]() ЃЈ4ЉtЃЉ2+
ЃЈ4ЉtЃЉ2+![]() ЃЈ4ЉtЃЉ+2ЃЌдйЗжЕуNдкЕуEзѓВрКЭгвВрСНжжЧщПіЃЌБэЪОГіNEЕФГЄЃЌРћгУNE=PEСаЗНГЬЧѓНтПЩЕУД№АИЃЎ
ЃЈ4ЉtЃЉ+2ЃЌдйЗжЕуNдкЕуEзѓВрКЭгвВрСНжжЧщПіЃЌБэЪОГіNEЕФГЄЃЌРћгУNE=PEСаЗНГЬЧѓНтПЩЕУД№АИЃЎ
ЃЈ1ЃЉЁпCЃЈ0ЃЌЉ2ЃЉЃЌ
ЁрOC=2ЃЌ
гЩtanЁЯBCO=![]() =2ЕУOB=4ЃЌ
=2ЕУOB=4ЃЌ
дђЕуBЃЈ4ЃЌ0ЃЉЃЌ
ЁпOB=4OAЃЌ
ЁрOA=1ЃЌ
дђAЃЈЉ1ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉНЋЕуAЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉДњШыy=ax2+bxЉ2ЃЌ
ЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК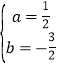 ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊy=![]() x2Љ
x2Љ![]() xЉ2ЃЛ
xЉ2ЃЛ
ЃЈ3ЃЉЩшЕуMЁЂЕуNЕФдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌдђAN=2tЁЂBM=![]() tЃЌ
tЃЌ
ЁпPEЁЭxжсЃЌ
ЁрPEЁЮOCЃЌ
ЁрЁЯBME=ЁЯBCOЃЌ
дђtanЁЯBME=tanЁЯBCOЃЌМД![]() =2ЃЌ
=2ЃЌ
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌ
ЃЌ
дђBE=tЃЌ
ЁрOE=OBЉBE=4ЉtЃЌ
ЁрPE=Љ[![]() ЃЈ4ЉtЃЉ2Љ
ЃЈ4ЉtЃЉ2Љ![]() ЃЈ4ЉtЃЉЉ2]=Љ
ЃЈ4ЉtЃЉЉ2]=Љ![]() ЃЈ4ЉtЃЉ2+
ЃЈ4ЉtЃЉ2+![]() ЃЈ4ЉtЃЉ+2ЃЌ
ЃЈ4ЉtЃЉ+2ЃЌ
ЂйЕуNдкЕуEзѓВрЪБЃЌМДЉ1+2tЃМ4ЉtЃЌНтЕУtЃМ![]() ЃЌ
ЃЌ
ДЫЪБNE=AO+OEЉAN=1+4ЉtЉ2t=5Љ3tЃЌ
ЁпЁїPNEЪЧЕШбќШ§НЧаЮЃЌ
ЁрPE=NEЃЌ
МДЉ![]() ЃЈ4ЉtЃЉ2+
ЃЈ4ЉtЃЉ2+![]() ЃЈ4ЉtЃЉ+2=5Љ3tЃЌ
ЃЈ4ЉtЃЉ+2=5Љ3tЃЌ
ећРэЃЌЕУЃКt2Љ11t+10=0ЃЌ
НтЕУЃКt=1Лђt=10ЃО![]() ЃЈЩсЃЉЃЛ
ЃЈЩсЃЉЃЛ
ЂкЕБЕуNдкЕуEгвВрЪБЃЌМДЉ1+2tЃО4ЉtЃЌНтЕУtЃО![]() ЃЌ
ЃЌ
гж![]() Чв2tЁм5ЃЌ
Чв2tЁм5ЃЌ
Ёр![]() ЃМtЁм
ЃМtЁм![]() ЃЌ
ЃЌ
ДЫЪБNE=ANЉAOЉOE=2tЉ1ЉЃЈ4ЉtЃЉ=3tЉ5ЃЌ
гЩPE=NEЕУЉ![]() ЃЈ4ЉtЃЉ2+
ЃЈ4ЉtЃЉ2+![]() ЃЈ4ЉtЃЉ+2=3tЉ5ЃЌ
ЃЈ4ЉtЃЉ+2=3tЉ5ЃЌ
ећРэЃЌЕУЃКt2+tЉ10=0ЃЌ
НтЕУЃКt=![]() ЃМ0ЃЌЩсШЅЃЛЛђt=
ЃМ0ЃЌЩсШЅЃЛЛђt=![]() ЃО
ЃО![]() ЃЌЩсШЅЃЛ
ЃЌЩсШЅЃЛ
злЩЯЃЌЕБt=1ЪБЃЌЁїPNEЪЧЕШбќШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌADЁЭBCгкЕуDЃЌCEЁЭABгкЕуE.

(1)ВТВтЁЯ1гыЁЯ2ЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
(2)ШчЙћЁЯABCЪЧЖлНЧЃЌШчЭМ2ЃЌ(1)жаЕФНсТлЪЧЗёЛЙГЩСЂЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯABCЃН90ЁуЃЌABЃН8ЃЌBCЃН6ЃЌЕуDЮЊACБпЩЯЕФЖЏЕуЃЌЕуDДгЕуCГіЗЂЃЌбиБпCAЯђЕуAдЫЖЏЃЌЕБдЫЖЏЕНЕуAЪБЭЃжЙЃЌШєЩшЕуDдЫЖЏЕФЪБМфЮЊtУыЃЎЕуDдЫЖЏЕФЫйЖШЮЊУПУы1ИіЕЅЮЛГЄЖШЃЎ

(1)ЕБtЃН2ЪБЃЌCDЃН ЃЌ ADЃН ЃЛ
(2)ЧѓЕБtЮЊКЮжЕЪБЃЌЁїCBDЪЧжБНЧШ§НЧаЮЃЌЫЕУїРэгЩЃЛ
(3)ЧѓЕБtЮЊКЮжЕЪБЃЌЁїCBDЪЧвдBDЛђCDЮЊЕзЕФЕШбќШ§НЧаЮЃПВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃашвЊЬэжУНЬЪІАьЙЋзРвЮAЁЂBСНаЭЙВ200ЬзЃЌвбжЊ2ЬзAаЭзРвЮКЭ1ЬзBаЭзРвЮЙВаш2000дЊЃЌ1ЬзAаЭзРвЮКЭ3ЬзBаЭзРвЮЙВаш3000дЊЃЎ
ЃЈ1ЃЉЧѓAЃЌBСНаЭзРвЮЕФЕЅМлЃЛ
ЃЈ2ЃЉШєашвЊAаЭзРвЮВЛЩйгк120ЬзЃЌBаЭзРвЮВЛЩйгк70ЬзЃЌЦНОљУПЬззРвЮашвЊдЫЗб10дЊЃЎЩшЙКТђAаЭзРвЮxЬзЪБЃЌзмЗбгУЮЊyдЊЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧѓГізмЗбгУзюЩйЕФЙКжУЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛНЧЕФСНБпгыСэвЛИіНЧЕФСНБпЦНааЃЌЗжБ№НсКЯЯТЭМЃЌЪдЬНЫїетСНИіНЧжЎМфЕФЙиЯЕЃЌВЂжЄУїФуЕФНсТл.
ЃЈ1ЃЉШчЭМЃЈ1ЃЉABЁЮEFЃЌBCЁЮDEЃЌЁЯ1гыЁЯ2ЕФЙиЯЕЪЧЃК____________ .

ЃЈ2ЃЉШчЭМЃЈ2ЃЉABЁЮEFЃЌBCЁЮDEЃЌ ЁЯ1гыЁЯ2ЕФЙиЯЕЪЧЃК____________

ЃЈ3ЃЉОЙ§ЩЯЪіжЄУїЃЌЮвУЧПЩвдЕУЕНвЛИіецУќЬтЃКШчЙћ____ _____ЃЌФЧУД____________.
ЃЈ4ЃЉШєСНИіНЧЕФСНБпЛЅЯрЦНааЃЌЧввЛИіНЧБШСэвЛИіНЧЕФ2БЖЩй30ЁуЃЌдђетСНИіНЧЗжБ№ЪЧЖрЩйЖШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌAB=ACЃЌADЪЧаББпЕФжаЯпЃЌEЁЂFЗжБ№ЪЧABЁЂACБпЩЯЕФЕуЧвDEЁЭDF.

ЃЈ1ЃЉЧѓжЄ:ЁїAEDЁеЁїCFDЃЛ
ЃЈ2ЃЉШєBE=8ЃЌCF=6ЃЌЧѓЁїDEFЕФУцЛ§ЃЛ
ЃЈ3ЃЉШєAB=aЃЌAE=xЃЌЧыгУКЌxЃЌaЕФДњЪ§ЪНБэЪОЁїDEFЕФУцЛ§S.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)ЧыФуЛГіКЏЪ§y=![]() x2-4x+10ЕФЭМЯѓ,гЩЭМЯѓФуФмЗЂЯжетИіКЏЪ§ОпгаФФаЉаджЪ?
x2-4x+10ЕФЭМЯѓ,гЩЭМЯѓФуФмЗЂЯжетИіКЏЪ§ОпгаФФаЉаджЪ?
(2)ЭЈЙ§ХфЗНБфаЮ,ЫЕГіКЏЪ§y=-2x2+8x-8ЕФЭМЯѓЕФПЊПкЗНЯђЁЂЖдГЦжсЁЂЖЅЕузјБъ,етИіКЏЪ§газюДѓжЕЛЙЪЧзюаЁжЕ?етИіжЕЪЧЖрЩй?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМAB=CDЃЌAD=BCЃЌЙ§OЕуЕФжБЯпНЛADгкEЃЌНЛBCгкFЃЌЭМжаШЋЕШШ§НЧаЮгаЃЈЁЁЁЁЃЉ

A. 4Жд B. 5Жд C. 6Жд D. 7Жд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌAЃЌEЃЌFЃЌCдквЛЬѕжБЯпЩЯЃЌAEЃНCFЃЌЙ§EЃЌFЗжБ№зїDEЁЭACЃЌBFЁЭACЃЌДЙзуЗжБ№ЮЊEЁЂFЃЌЧвABЃНCDЃЎ

ЃЈ1ЃЉЁїABFгыЁїCDEШЋЕШТ№ЃПЮЊЪВУДЃП
ЃЈ2ЃЉЧѓжЄЃКEGЃНFGЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com