
【题目】(1)请你画出函数y=![]() x2-4x+10的图象,由图象你能发现这个函数具有哪些性质?
x2-4x+10的图象,由图象你能发现这个函数具有哪些性质?
(2)通过配方变形,说出函数y=-2x2+8x-8的图象的开口方向、对称轴、顶点坐标,这个函数有最大值还是最小值?这个值是多少?
【答案】(1)见解析;(2)见解析.
【解析】
(1)在坐标系中画出函数图象,再从开口方向、对称轴、顶点坐标及增减性阐述其性质;(2)利用配方法把y=-2x2+8x-8化为顶点式,根据函数的性质直接写出开口方向、对称轴、顶点坐标及最值即可.
解:(1)函数图象如图所示:
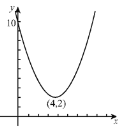
性质有: ①该函数图象的开口向上,对称轴为直线x=4,顶点(4,2). ②当x>4时,y随x的增大而增大;当x<4时,y随x的增大而减小.③当x=4时,y最小值=2.
(2)y=-2x2+8x-8=-2(x-2)2
.该函数图象的开口向下,对称轴为直线x=2,顶点(2,0).
∵a=-2<0,∴y有最大值,当x=2时,y最大值=0.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
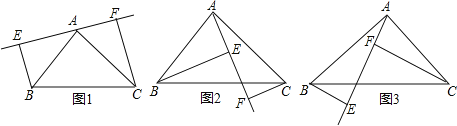
(1)如图1,当EF与斜边BC不相交时,请证明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF、BE、CF之间的数量关系,并说明理由;
(3)如图3,猜想EF、BE、CF之间又存在怎样的数量关系,写出猜想,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,﹣2),OB=4OA,tan∠BCO=2.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M、N分别是线段BC、AB上的动点,点M从点B出发以每秒![]() 个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?
个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
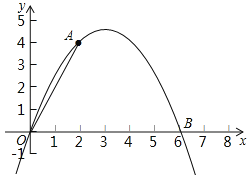
【题目】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将使结论成立的条件或理由填写在横线上或括号内.
如图,![]() 中,
中,![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 作
作![]() , 交
, 交![]() 的延长线于点
的延长线于点![]() .
.
求证:![]() 是
是![]() 的中点.
的中点.

证明:![]()
![]() (已知)
(已知)
![]()
![]()
![]() 是边
是边![]() 的中点
的中点
![]()
在![]() 和
和![]() 中
中

![]()
![]()
![]()
![]() 是
是![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式![]() ,........请按照上述三个等式及其变化过程,回答下列问题。
,........请按照上述三个等式及其变化过程,回答下列问题。
(1)猜想![]() ________________.
________________.
(2)猜想_____________________=![]() .
.
(3)试猜想第N个等式为_____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都和西安两地之间的铁路交通设有高铁列车和普快列车两种车次,某天一辆普快从西安出发匀速驶向成都,同时另一辆高铁从成都出发匀速驶向西安,两车与成都的距离![]() (千米)与行驶时间t(时)之间的关系如图所示.
(千米)与行驶时间t(时)之间的关系如图所示.
t | 0 | 1 | 2 | 4 | … |
S1 | 666 | 546 | 426 | 186 | … |

(1)西安与成都的距离为______千米,普通快车到达成都所用时间为_______小时;
(2)求高铁从成都到西安的距离![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)在成都、西安两地之间有一条隧道,高铁经过这条隧道时,两车相距74千米,求西安与这条隧道之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) .
.
(2)(﹣2a)3﹣(﹣a)(3a)2.
(3)(x+2)2﹣(x﹣1)(x﹣2).
(4)(a+b)2(a﹣b)2.
(5)(a﹣3)(a+3)(a2+9).
(6)(m﹣2n+3)(m+2n﹣3).
(7) .
.
(8)![]() .
.
(9)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com