
【题目】计算
(1) .
.
(2)(﹣2a)3﹣(﹣a)(3a)2.
(3)(x+2)2﹣(x﹣1)(x﹣2).
(4)(a+b)2(a﹣b)2.
(5)(a﹣3)(a+3)(a2+9).
(6)(m﹣2n+3)(m+2n﹣3).
(7) .
.
(8)![]() .
.
(9)![]() .
.
【答案】(1)-1;(2)a3;(3)7x+2;(4)a4﹣2a2b2+b4;(5)a4﹣81;(6)m2﹣4n2﹣9+12n;(7)3![]() ﹣3;(8)﹣2
﹣3;(8)﹣2![]() ;(9)5﹣
;(9)5﹣![]()
【解析】
(1)直接利用乘方运算、零指数幂的性质以及负整数指数幂的性质分别化简得出答案;
(2)直接利用积的乘方运算法则化简,进而得出答案;
(3)直接利用整式的乘法运算法则计算得出答案;
(4)直接利用积的乘方和乘法公式计算得出答案;
(5)直接利用乘法公式计算得出答案;
(6)将原式变形,然后利用乘法公式计算得出答案;
(7)直接利用算术平方根、立方根以及负整数指数幂的性质分别化简得出答案;
(8)直接利用绝对值、零指数幂的性质、二次根式的性质分别化简得出答案;
(9)直接利用乘法公式计算得出答案.
(1)原式=﹣4+1+2=﹣1;
(2)原式=﹣8a3+9a3=a3;
(3)原式=x2+4x+4﹣(x2﹣3x+2)=7x+2;
(4)原式=(a2﹣b2)2=a4﹣2a2b2+b4;
(5)原式=(a2﹣9)(a2+9)=a4﹣81;
(6)原式=[m﹣(2n﹣3)][m+(2n﹣3)]=m2﹣(2n﹣3)2=m2﹣4n2﹣9+12n;
(7)原式=2![]() ﹣3+
﹣3+![]() =3
=3![]() ﹣3;
﹣3;
(8)原式=![]() ﹣1+1﹣6×
﹣1+1﹣6×![]() =﹣2
=﹣2![]() ;
;
(9)原式=4﹣5+4+2﹣4![]() ﹣
﹣![]() =5﹣
=5﹣![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)请你画出函数y=![]() x2-4x+10的图象,由图象你能发现这个函数具有哪些性质?
x2-4x+10的图象,由图象你能发现这个函数具有哪些性质?
(2)通过配方变形,说出函数y=-2x2+8x-8的图象的开口方向、对称轴、顶点坐标,这个函数有最大值还是最小值?这个值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.

(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为E、F,且AB=CD.

(1)△ABF与△CDE全等吗?为什么?
(2)求证:EG=FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,
,![]() cm,
cm,![]() cm,若以C为圆心,以2cm为半径作圆,则点A在⊙C_____;点B在⊙C________;若以AB为直径作⊙O,则点C在⊙O_______.
cm,若以C为圆心,以2cm为半径作圆,则点A在⊙C_____;点B在⊙C________;若以AB为直径作⊙O,则点C在⊙O_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
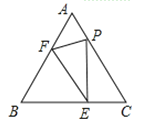
【题目】如图,等边![]() 的边长为
的边长为![]() ,
,![]() 是边
是边![]() 上的动点,
上的动点,![]() 交边
交边![]() 于点
于点![]() ,在边
,在边![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请直接写出图中与线段![]() 相等的两条线段;(不再另外添加辅助线)
相等的两条线段;(不再另外添加辅助线)
(2)探究:当点![]() 在什么位置时,四边形
在什么位置时,四边形![]() 是平行四边形?并判断四边形
是平行四边形?并判断四边形![]() 是什么特殊的平行四边形,请说明理由;
是什么特殊的平行四边形,请说明理由;
(3)在(2)的条件下,以点![]() 为圆心,
为圆心,![]() 为半径作圆,根据
为半径作圆,根据![]() 与平行四边形
与平行四边形![]() 四条边交点的总个数,求相应的
四条边交点的总个数,求相应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小正方形组成的的网格纸中,四边形ABCD和四边形A2B2C2D2的位置如图所示.

(1)现把四边形ABCD绕C点按顺时针方向旋转90°,画出相应的图形A1B1C1D1,
(2)若四边形A1B1C1D1平移后,与四边形A2B2C2D2成轴对称,写出满足要求的一种平移方法,并画出平移后的图形A3B3C3D3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把![]() 向上平移4个单位长度,再向右平移3个单位长度得
向上平移4个单位长度,再向右平移3个单位长度得![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
(1)在图上画出![]() ;
;
(2)写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)请直接写出线段![]() 在两次平移中扫过的总面积.
在两次平移中扫过的总面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com