
����Ŀ����֪һ�ǵ���������һ���ǵ�����ƽ�У��ֱ�����ͼ����̽����������֮��Ĺ�ϵ����֤����Ľ���.
��1����ͼ��1��AB��EF��BC��DE����1���2�Ĺ�ϵ�ǣ�____________ .

��2����ͼ��2��AB��EF��BC��DE�� ��1���2�Ĺ�ϵ�ǣ�____________

��3����������֤�������ǿ��Եõ�һ�������⣺���____ _____����ô____________.
��4���������ǵ�������ƽ�У���һ���DZ���һ���ǵ�2����30�������������Ƿֱ��Ƕ��ٶȣ�
���𰸡���1����1=��2��֤������������2����1+��2=180����֤������������3��һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У�����������Ȼ�����4���������Ƿֱ���30����30����70����110����
��������
��1��������ֱ��ƽ�У��ڴ�����ȣ��������1=��2��
��2��������ֱ��ƽ�У��ڴ�����ȼ�ͬ���ڽǻ����������1+��2=180����
��3���ɣ�1����2���ɵó����ۣ�
��4���ɣ�3�����г����̣�����ǵĶ�����
�⣺��1��AB��EF��BC��DE����1���2�Ĺ�ϵ�ǣ���1=��2
֤������AB��EF
���1=��BCE
��BC��DE
���2=��BCE
���1=��2��
��2��AB��EF��BC��DE����1���2�Ĺ�ϵ�ǣ���1+��2=180����
֤������AB��EF
���1=��BCE
��BC��DE
���2+��BCE=180��
���1+��2=180����
��3����������֤�������ǿ��Եõ�һ�������⣺���һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У���ô����������Ȼ���
��4���⣺������һ����Ϊx�����з��̵�x=2x-30��x+2x-30=180��
��x=30��x=70��
����2x-30=30��110��
���������Ƿֱ���30����30����70����110����


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���PQR�ǡ�ABC����ij�ֱ任��õ���ͼ�Σ����е�A���P����B���Q����C���R�Ƕ�Ӧ�ĵ㣬�����ֱ任�£�
(1)ֱ��д�����и��������
��A(____��_____)��P(_____��_____)��B(_____��_____)��Q(______��_____)��C(_____��______)��R(______��______)
������֮��Ĺ�ϵ�ǣ�______(����������ֱ��д��)
(2)���������ϵ�У�������ABC����һ��M����M�������ֱ任��õ���N����N��������PQR�ڣ�����M��N������M(![]() ��6(a+b)��10)��N(1��
��6(a+b)��10)��N(1��![]() ��4(b��2a)��6)�������x�IJ���ʽ
��4(b��2a)��6)�������x�IJ���ʽ![]() ��
��![]() ��b��1�Ľ⼯��
��b��1�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı�AB�������ϣ������ϵ�A��ʾ����Ϊ-1��������ABCD�����Ϊ16��
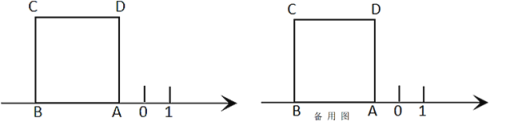
(1)�����ϵ�B��ʾ����Ϊ___��
(2)��������ABCD������ˮƽ�ƶ����ƶ���������μ�ΪA��B��C��D�䣬�ƶ����������A��B��C��D����ԭ������ABCD�ص����ֵ����ΪS��
�ٵ�S=4ʱ������ͼ�Σ�����������ϵ�A���ʾ������
����������ABCD���ƶ��ٶ�Ϊÿ��2����λ���ȣ���EΪ�߶�AA����е㣬��F���߶�BB���ϣ���BF=![]() BB�䣮����t���E��F����ʾ������Ϊ�෴����ֱ��д��t��ֵ��
BB�䣮����t���E��F����ʾ������Ϊ�෴����ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ�д�С����״��ͬ��3�������2���������dz�ֽ��ȣ�
��1�������������ȡ1�����Ǻ�����ǰ��������� ���¼��������������ȡ1�����Ǻ��������� ���¼���
��2�����������ȡ1����ǡ���Ǻ���ĸ������� ����
��3��ѧУ�����ڼס�������ͬѧ��ѡȡһ����Ϊѧ���������ԣ��ƶ����¹��Ӻ�������ȡ������������ͬɫ����ѡ�ף���������ɫ����ѡ�ң�����Ϊ�������ƽ�������б�������״ͼ������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��CD��ֱ��L��ֱ��AB��CD�ֱ��ڵ�E��F��ֱ��L����һ����P��

��1����ͼ1����P��E��F֮���˶�ʱ����PMB����MPN����PND֮����ʲô��ϵ����˵�����ɣ�
��2������P��E��F��������˶�ʱ����ͼ2��ͼ3��P����E��F���غϣ�����ֱ��д����PMB����MPN����PND֮����ʲô��ϵ������д���ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx��2��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��0����2����OB=4OA��tan��BCO=2��
��1����A��B��������ꣻ
��2���������ߵĽ���ʽ��
��3����M��N�ֱ����߶�BC��AB�ϵĶ��㣬��M�ӵ�B������ÿ��![]() ����λ���ٶ����C�˶���ͬʱ��N�ӵ�A������ÿ��2����λ���ٶ����B�˶�������M��N�е�һ�㵽���յ�ʱ������ͬʱֹͣ�˶�������M��MP��x���ڵ�E�����������ڵ�P�����M����N���˶�ʱ��Ϊt��s������tΪ����ʱ����PNE�ǵ��������Σ�
����λ���ٶ����C�˶���ͬʱ��N�ӵ�A������ÿ��2����λ���ٶ����B�˶�������M��N�е�һ�㵽���յ�ʱ������ͬʱֹͣ�˶�������M��MP��x���ڵ�E�����������ڵ�P�����M����N���˶�ʱ��Ϊt��s������tΪ����ʱ����PNE�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
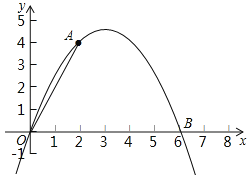
����Ŀ����ͼ�����κ���y=ax2+bx��ͼ����A��2��4����B��6��0����
��1����a��b��ֵ��
��2����C�Ǹö��κ���ͼ����A��B����֮���һ���㣬������Ϊx��2��x��6����д���ı���OACB�����S���ڵ�C�ĺ�����x�ĺ�������ʽ������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����и�ʽ![]() ��........�밴������������ʽ����仯���̣��ش��������⡣
��........�밴������������ʽ����仯���̣��ش��������⡣
��1������![]() ________________.
________________.
��2������_____________________=![]() .
.
��3���Բ����N����ʽΪ_____________________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDֽƬ�У���֪��A=160�㣬��B=30�㣬��C=60�����ı���ABCDֽƬ�ֱ���EF��GH��OP��MN�۵���ʹA��A�䡢B��B�䡢C��C�䡢D��D���غϣ����1+��2+��3+��4+��5+��6+��7����8��ֵ�ǣ�������

A. 600�� B. 700�� C. 720�� D. 800��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com