
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC. 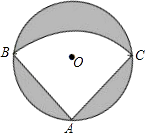
(1)求被剪掉阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
【答案】
(1)解:如图,连接BC,

∵∠BAC=90°,
∴BC为⊙O的直径,即BC=1m,
又∵AB=AC,
∴AB= ![]() BC=
BC= ![]() .
.
∴S阴影部分=S⊙O﹣S扇形ABC=π×( ![]() )2﹣
)2﹣ ![]() =
= ![]() (平方米)
(平方米)
(2)解:设底面圆的半径为r,则 ![]() π=2πr,
π=2πr,
∴r= ![]() m
m
圆锥的底面圆的半径长为 ![]() 米
米
【解析】(1)由∠BAC=90°,得BC为⊙O的直径,即BC=1m;又由AB=AC,得到AB= ![]() BC=
BC= ![]() ,而S阴影部分=S⊙O﹣S扇形ABC , 然后根据扇形和圆的面积公式进行计算即可;(2)扇形的半径是2sin45°=
,而S阴影部分=S⊙O﹣S扇形ABC , 然后根据扇形和圆的面积公式进行计算即可;(2)扇形的半径是2sin45°= ![]() ,扇形的弧长l=
,扇形的弧长l= ![]() =
= ![]() ,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
【考点精析】本题主要考查了扇形面积计算公式和圆锥的相关计算的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
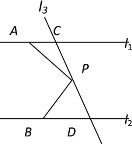
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线CD上的一个动点。
(1)如果点P运动到C、D之间时,试探究∠PAC,∠APB,∠PBD之间的关系,并说明理由。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),∠PAC,∠APB,∠PBD之间 的关系是否发生改变?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 . 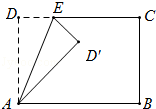
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ![]() ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).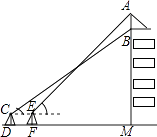
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房,旅游团如何安排住宿才能够使得住宿费最低,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com