
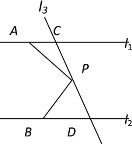
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线CD上的一个动点。
(1)如果点P运动到C、D之间时,试探究∠PAC,∠APB,∠PBD之间的关系,并说明理由。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),∠PAC,∠APB,∠PBD之间 的关系是否发生改变?请说明理由。
【答案】(1)P点在C、D之间运动时,则有∠APB=∠PAC+∠PBD,理由详见解析;(2)详见解析.
【解析】
(1)当P点在C、D之间运动时,首先过点P作![]() ,由
,由![]() ,可得
,可得![]() ,根据两直线平行,内错角相等,即可求得: ∠APB=∠PAC+∠PBD;
,根据两直线平行,内错角相等,即可求得: ∠APB=∠PAC+∠PBD;
(2)当点P在C、D两点的外侧运动时,则有两种情形,由直线![]() ,根据两直线平行,内错角相等,同位角相等与三角形外角的性质,可分别求得:∠APB=∠PAC-∠PBD和∠APB=∠PBD-∠PAC.
,根据两直线平行,内错角相等,同位角相等与三角形外角的性质,可分别求得:∠APB=∠PAC-∠PBD和∠APB=∠PBD-∠PAC.
解:(1)若P点在C、D之间运动时,则有∠APB=∠PAC+∠PBD.理由是:
如图,过点P作PE∥l1,则∠APE=∠PAC,
又因为l1∥l2,所以PE∥l2,
所以∠BPE=∠PBD,
所以∠APE+∠BPE=∠PAC+∠PBD,
即∠APB=∠PAC+∠PBD.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),则有两种情形:
①如图1,有结论:∠APB=∠PAC-∠PBD.理由是:
过点P作PE∥l1,则∠APE=∠PAC
又因为l1∥l2,所以PE∥l2
所以∠BPE=∠PBD
所以∠APB=∠APE-∠BPE
即∠APB=∠PAC-∠PBD.
②如图2,有结论:∠APB=∠PBD-∠PAC.理由是:
过点P作PE∥l2,则∠BPE=∠PBD
又因为l1∥l2,所以PE∥l1
所以∠APE=∠PAC
所以∠APB=∠BPE-∠APE
即∠APB=∠PBD-∠PAC.


科目:初中数学 来源: 题型:
【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P是△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线y= ![]() (x>0)上的任意一点,点N是x轴正半轴上的任意一点.
(x>0)上的任意一点,点N是x轴正半轴上的任意一点.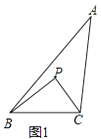
(1)如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是( ![]() ,3),点N的坐标是(
,3),点N的坐标是( ![]() ,0)时,求点P的坐标;
,0)时,求点P的坐标;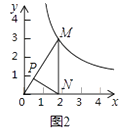
(2)如图3,当点M的坐标是(3, ![]() ),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
(3)是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B2C2(△ABC与△A1B2C2在位似中心O点的两侧,A,B,C的对应点分别是A1 , B2 , C2).
(2)利用方格纸标出△A1B2C2外接圆的圆心P,P点坐标是⊙P的半径= . (保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E. 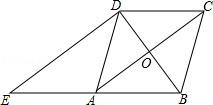
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y= ![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
的图象上,OA=2,OC=6,则正方形ADEF的边长为 . 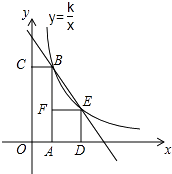
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC. 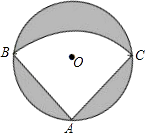
(1)求被剪掉阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A,B,C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整),请你结合图中的信息,解答下列问题: 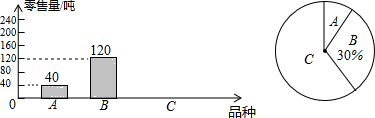
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)补全图1的统计图并计算图2中A所在扇形的圆心角的度数;
(3)某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年世界环境日(即6月5日),某市发布了一份空气质量的抽样调查报告,其中该市2~5月随机调查的25天各空气质量级别的天数如下表所示:

(1)试估计该市今年的空气质量主要是哪个级别?
(2)根据抽样数据,预测该市今年空气质量级别为优和良的天数共约为多少天?
(3)根据调查报告,试对有关部门提一条建设“绿色城市”的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com