
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y= ![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
的图象上,OA=2,OC=6,则正方形ADEF的边长为 . 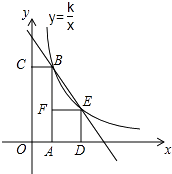
科目:初中数学 来源: 题型:
【题目】完成下列证明过程:
如图,∠1=∠2,AC平分∠DAB.
![]()
求证:DC∥AB.
证明:因为AC平分∠DAB(已知),
所以∠1=∠3(_____________ ).
又因为∠1=∠2(____________),
所以∠2=∠3(______________),
所以DC∥AB(________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
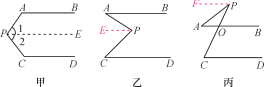
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题“计算:(-![]() )÷(
)÷(![]()
![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]()
![]() )÷(
)÷(![]() )=(
)=(![]()
![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]()
![]() )=
)=![]() .
.
(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-![]() )÷(
)÷(![]()
![]() +
+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
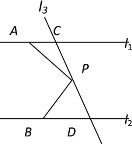
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线CD上的一个动点。
(1)如果点P运动到C、D之间时,试探究∠PAC,∠APB,∠PBD之间的关系,并说明理由。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),∠PAC,∠APB,∠PBD之间 的关系是否发生改变?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题: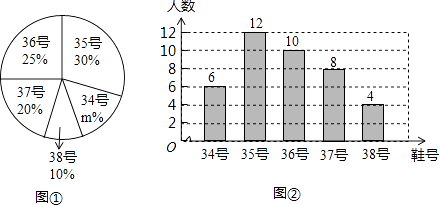
(1)本次接受随机抽样调查的学生人数为 , 图①中m的值为;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ![]() ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).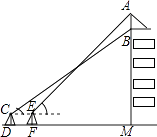
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子元件厂准备生产4600个电子元件,甲车间独立生产一半后,由于要尽快投入市场,乙车间也加入了该电子元件的生产.若乙车间每天生产的电子元件的个数是甲车间每天生产的电子元件的个数的1.3倍,结果共用33天完成了任务.问:甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可列方程为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com