
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题: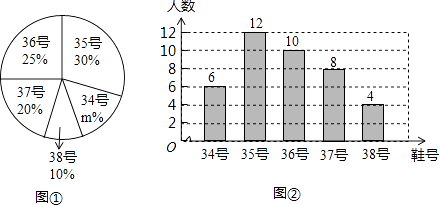
(1)本次接受随机抽样调查的学生人数为 , 图①中m的值为;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
【答案】
(1)40;15
(2)
解:∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35;
∵将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为36,
∴中位数为 ![]() =36
=36
(3)
解:∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据,估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号
【解析】解:(1)本次接受随机抽样调查的学生人数为6+12+10+8+4=40,图①中m的值为100﹣30﹣25﹣20﹣10=15;
故答案为:40;15;
(1)根据条形统计图求出总人数即可;由扇形统计图以及单位1,求出m的值即可;(2)找出出现次数最多的即为众数,将数据按照从小到大顺序排列,求出中位数即可;(3)根据题意列出算式,计算即可得到结果.


科目:初中数学 来源: 题型:
【题目】观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( ) 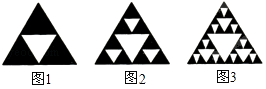
A.121
B.362
C.364
D.729
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.

(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从永福超市出发负责送货,向东走了5千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了9.5千米到达小刚家,最后返回永福超市.
![]()
(1)以永福超市为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.6升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y= ![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
的图象上,OA=2,OC=6,则正方形ADEF的边长为 . 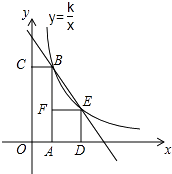
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),AB中点P的坐标为(xp , yp).由xp﹣x1=x2﹣xp , 得xp= ![]() ,同理yp=
,同理yp= ![]() ,所以AB的中点坐标为(
,所以AB的中点坐标为( ![]() ,
, ![]() ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB= ![]() .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题: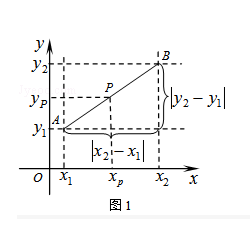
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为 , MN= .
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.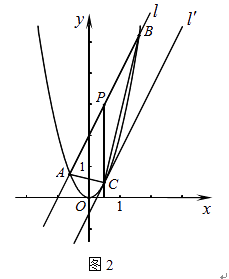
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com