
【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P是△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线y= ![]() (x>0)上的任意一点,点N是x轴正半轴上的任意一点.
(x>0)上的任意一点,点N是x轴正半轴上的任意一点.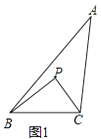
(1)如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是( ![]() ,3),点N的坐标是(
,3),点N的坐标是( ![]() ,0)时,求点P的坐标;
,0)时,求点P的坐标;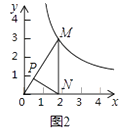
(2)如图3,当点M的坐标是(3, ![]() ),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
(3)是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵∠ONP=∠M,∠NOP=∠MON,
∴△NOP∽△MON,
∴点P是△MON的自相似点;
过P作PD⊥x轴于D,则tan∠POD= ![]() ,
,
∴∠AON=60°,
∵当点M的坐标是( ![]() ,3),点N的坐标是(
,3),点N的坐标是( ![]() ,0),
,0),
∴∠MNO=90°,
∵△NOP∽△MON,
∴∠NPO=∠MNO=90°,
在Rt△OPN中,OP=ONcos60°= ![]() ,
,
∴OD=OPcos60°= ![]() ×
× ![]() =
= ![]() ,PD=OPsin60°=
,PD=OPsin60°= ![]() ×
× ![]() =
= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
(2)
解:作ME⊥x轴于H,如图3所示:
∵点M的坐标是(3, ![]() ),点N的坐标是(2,0),
),点N的坐标是(2,0),
∴OM= ![]() =2
=2 ![]() ,直线OM的解析式为y=
,直线OM的解析式为y= ![]() x,ON=2,∠MOH=30°,
x,ON=2,∠MOH=30°,
分两种情况:
①如图3所示:
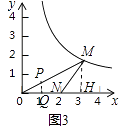
∵P是△MON的相似点,
∴△PON∽△NOM,作PQ⊥x轴于Q,
∴PO=PN,OQ= ![]() ON=1,
ON=1,
∵P的横坐标为1,
∴y= ![]() ×1=
×1= ![]() ,
,
∴P(1, ![]() );
);
②如图4所示:
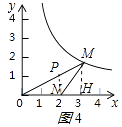
由勾股定理得:MN= ![]() =2,
=2,
∵P是△MON的相似点,
∴△PNM∽△NOM,
∴ ![]()
![]() ,
,
解得:PN= ![]() ,
,
即P的纵坐标为 ![]() ,代入y=
,代入y= ![]() 得:
得: ![]() =
= ![]() x,
x,
解得:x=2,
∴P(2, ![]() );
);
综上所述:△MON的自相似点的坐标为(1, ![]() )或(2,
)或(2, ![]() );
);
(3)
解:存在点M和点N,使△MON无自相似点,M( ![]() ,3),N(2
,3),N(2 ![]() ,0);理由如下:
,0);理由如下:
∵M( ![]() ,3),N(2
,3),N(2 ![]() ,0),
,0),
∴OM=2 ![]() =ON,∠MON=60°,
=ON,∠MON=60°,
∴△MON是等边三角形,
∵点P在△ABC的内部,
∴∠PBC≠∠A,∠PCB≠∠ABC,
∴存在点M和点N,使△MON无自相似点.
【解析】(1)由∠ONP=∠M,∠NOP=∠MON,得出△NOP∽△MON,证出点P是△MON的自相似点;过P作PD⊥x轴于D,则tan∠POD= ![]() ,求出∠AON=60°,由点M和N的坐标得出∠MNO=90°,由相似三角形的性质得出∠NPO=∠MNO=90°,在Rt△OPN中,由三角函数求出OP=
,求出∠AON=60°,由点M和N的坐标得出∠MNO=90°,由相似三角形的性质得出∠NPO=∠MNO=90°,在Rt△OPN中,由三角函数求出OP= ![]() ,OD=
,OD= ![]() ,PD=
,PD= ![]() ,即可得出答案;(2)作ME⊥x轴于H,由勾股定理求出OM=2
,即可得出答案;(2)作ME⊥x轴于H,由勾股定理求出OM=2 ![]() ,直线OM的解析式为y=
,直线OM的解析式为y= ![]() x,ON=2,∠MOH=30°,分两种情况:①作PQ⊥x轴于Q,由相似点的性质得出PO=PN,OQ=
x,ON=2,∠MOH=30°,分两种情况:①作PQ⊥x轴于Q,由相似点的性质得出PO=PN,OQ= ![]() ON=1,求出P的纵坐标即可;②求出MN=
ON=1,求出P的纵坐标即可;②求出MN= ![]() =2,由相似三角形的性质得出
=2,由相似三角形的性质得出 ![]() ,求出PN=
,求出PN= ![]() ,在求出P的横坐标即可;(3)证出OM=2
,在求出P的横坐标即可;(3)证出OM=2 ![]() =ON,∠MON=60°,得出△MON是等边三角形,由点P在△ABC的内部,得出∠PBC≠∠A,∠PCB≠∠ABC,即可得出结论.
=ON,∠MON=60°,得出△MON是等边三角形,由点P在△ABC的内部,得出∠PBC≠∠A,∠PCB≠∠ABC,即可得出结论.
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
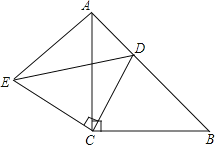
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,
(1)求证:△ACE≌△BCD;
(2)若AE=3,AD=2,求DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3. 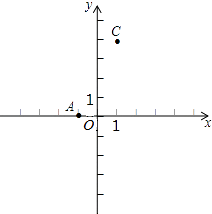
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
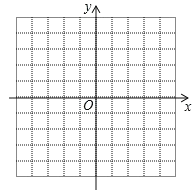
【题目】在平面直角坐标系中描出点 A(﹣2,0)、B(3,1)、C(2,3),将各点用线段依次 连接起来,并解答如下问题:
(1)在平面直角坐标系中画出△ A′B′C′,使它与△ ABC 关于 x 轴对称,并直接写出△ A′B′C′三个顶点的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
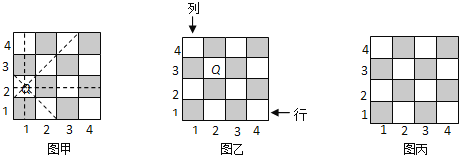
【题目】国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程:
如图,∠1=∠2,AC平分∠DAB.
![]()
求证:DC∥AB.
证明:因为AC平分∠DAB(已知),
所以∠1=∠3(_____________ ).
又因为∠1=∠2(____________),
所以∠2=∠3(______________),
所以DC∥AB(________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上 A点表示的数是 a ,B 点表示的数是b ,且 ab满足|a 8|b-220.动线段 CD=4(点 D 在点 C 的右侧),从点 C与点 A重合的位置出发,以每秒 2 个单位的速度向右运动,运动时间为 t秒.
(1)求a,b的值, 运动过程中,点 D 表示的数是多少,(用含有 t 的代数式表示)
(2)在 B、C、D 三个点中,其中一个点是另外两个点为端点的线段的中点,求 t 的值;
(3)当线段 CD 在线段 AB上(不含端点重合)时,如图,图中所有线段的和记作为 S, 则 S的值是否随时间 t 的变化而变化?若变化,请说明理由;若不变,请求出 S值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
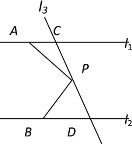
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线CD上的一个动点。
(1)如果点P运动到C、D之间时,试探究∠PAC,∠APB,∠PBD之间的关系,并说明理由。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),∠PAC,∠APB,∠PBD之间 的关系是否发生改变?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com