
【题目】如图①,若AB∥CD,点P在AB,CD外部,则有∠D=∠BOD,又因为∠BOD是△POB的外角,故∠BOD=∠BPD+∠B,得∠BPD=∠D﹣∠B.
探究一:将点P移到AB,CD内部,如图②,则∠BPD,∠B,∠D之间有何数量关系?并证明你的结论;
探究二:在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD延长线于点Q,如图③,则∠BPD,∠B,∠PDQ,∠BQD之间又有何数量关系?并证明你的结论;
探究三:在图④中,直接根据探究二的结论,写出∠A+∠B+∠C+∠D+∠E+∠F的度数.
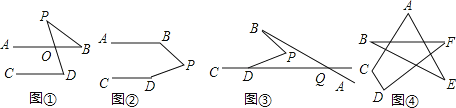
【答案】探究一:∠B+∠BPD+∠D=360°;探究二:∠BPD=∠B+∠PDQ+∠BQD;探究三:360°.
【解析】
试题分析:探究一,过点P作PE∥AB,根据平行线的性质可知∠B+∠BPE=180°,∠D+∠EPD=180°,即∠B+∠BPD+∠D=360°.
探究二,连接QP并延长至E,根据∠BPE是△BPQ的一个外角,得到∠BPE=∠BQP+∠B.同理得到∠EPD=∠DQP+∠PDQ,从而∠BPD=∠B+∠PDQ+∠BQD.
探究三,根据三角形外角性质和四边形的内角和等于360°得出即可.
探究一,∠B+∠BPD+∠D=360°,
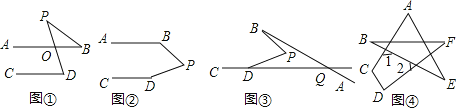
证明:过点P作PE∥AB,如图②,
∴∠B+∠BPE=180°,
又∵AB∥CD,
∴PE∥CD,
∴∠D+∠EPD=180°,
∴∠B+∠BPE+∠D+∠EPD=360°,
即∠B+∠BPD+∠D=360°;
探究二,∠BPD=∠B+∠PDQ+∠BQD,
证明:连接QP并延长至E,如图③,
∵∠BPE是△BPQ的一个外角,
∴∠BPE=∠BQP+∠B.
同理:∠EPD=∠DQP+∠PDQ.
∴∠BPE+∠EPD=∠BQP+∠B+∠DQP+∠PDQ.
即:∠BPD=∠B+∠PDQ+∠BQD;
探究三,如图④,∵∠1=∠A+∠E,∠2=∠B+∠F,∠1+∠2+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x)2=28.8
D.20+20(1+x)+20(1+x)2=28.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
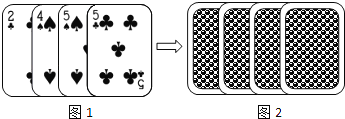
【题目】四张扑克牌的牌面如图1所示,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列推理正确的是( )
A.∵a // d, b // c,∴c // d
B.∵ a // c,b // d,∴ c // d
C.∵ a // b,a // c,∴ b // c
D.∵ a // b,c // d,∴ a // c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正确的是 (填编号)
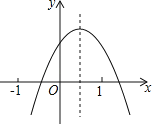
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com