
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C做⊙O 的切线,与AE的延长线交于点D,且AD⊥CD.
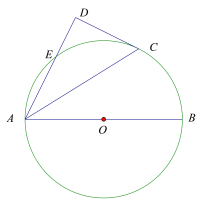
(1)求证:AC平分∠DAB;
(2)若AB=10,CD=4,求DE的长.
【答案】(1)见解析;(2)DE=2
【解析】
(1)连接OC,利用切线的性质可得出OC∥AD,再根据平行线的性质得出∠DAC=∠OCA,又因为∠OCA=∠OAC,继而可得出结论;
(2)方法一:连接BE交OC于点H,可证明四边形EHCD为矩形,再根据垂径定理可得出![]() ,得出
,得出![]() ,从而得出
,从而得出![]() ,再通过三角形中位线定理可得出
,再通过三角形中位线定理可得出![]() ,继而得出结论
,继而得出结论![]() ;方法二:连接BC、EC,可证明△ADC∽△ACB,利用相似三角形的性质可得出AD=8,再证△DEC∽△DCA,从而可得出结论;方法三:连接BC、EC,过点C做CF⊥AB,垂足为F,利用已知条件得出OF=3,再证明△DEC≌△CFB,利用全等三角形的性质即可得出答案.
;方法二:连接BC、EC,可证明△ADC∽△ACB,利用相似三角形的性质可得出AD=8,再证△DEC∽△DCA,从而可得出结论;方法三:连接BC、EC,过点C做CF⊥AB,垂足为F,利用已知条件得出OF=3,再证明△DEC≌△CFB,利用全等三角形的性质即可得出答案.
解:(1)证明:连接OC,

∵CD切☉O于点C
∴OC⊥CD
∵AD⊥CD
∴∠D=∠OCD=90°
∴∠D+∠OCD=180°
∴OC∥AD
∴∠DAC=∠OCA
∵OA=OC
∴∠OCA=∠OAC
∴∠DAC=∠OAC
∴AC平分DAB
(2)方法1:连接BE交OC于点H
∵AB是☉O直径
∴∠AEB=90°
∴∠DEC=90°
∴四边形EHCD为矩形
∴CD=EH=4
DE=CH
∴∠CHE=90°
即OC⊥BH
∴EH=BE=4
∴BE=8
∴在Rt△AEB中
AE![]() =6
=6
∵EH=BH
AO=BO
∴OH=![]() AE=3
AE=3
∴CH=2
∴DE=2
方法2:
连接BC、EC
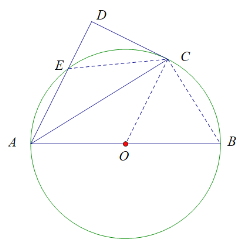
∵AB是直径
∴∠ACB=90°
∴∠D=∠ACB
∵∠DAC=∠CAB
∴△ADC∽△ACB
∴![]()
∠B=∠DCA
∴AC2=10·AD
∵AC2=AD2+CD2
∴10·AD=AD2+16
∴AD=2舍AD=8
∵四边形ABCE内接于☉O
∴∠B+∠AEC=180°
∵∠DEC+∠AEC=180°
∴∠B=∠DEC
∴∠DEC=∠DCA
∵∠D=∠D
∴△DEC∽△DCA
∴![]()
∴CD2=AD·DE
∴16=8·DE
∴DE=2;
方法3:
连接BC、EC,过点C做CF⊥AB,垂足为F
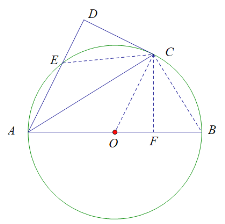
∵CD⊥AD,∠DAC=∠CAB
∴CD=CF=4,∠D=∠CFB=90°
∵AB=10
∴OC=OB=5
∴OF=3
∴BF=OB-OF=5-3=2
∵四边形ABCE内接于☉O
∴∠B+∠AEC=180°
∵∠DEC+∠AEC=180°
∴∠B=∠DEC
∴△DEC≌△CFB
∴DE=FB=2.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
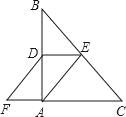
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】10个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报2的人心里想的数是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图乙,![]() 和
和![]() 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
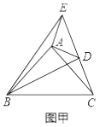
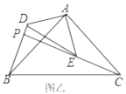
(1)如图甲,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 、
、![]() 、
、![]() 在同一条直线上时,连接
在同一条直线上时,连接![]() 、
、![]() ,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
(2)若![]() ,
,![]() ,把
,把![]() 绕点
绕点![]() 旋转.
旋转.
①当![]() 时,求
时,求![]() 的长;
的长;
②直接写出旋转过程中线段![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
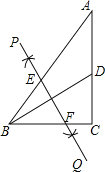
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于![]() BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.某车行经营的 A 型车去年 4 月份销售总额为 3.2 万元,今年经过改造升级后 A 型车每辆销售价比去年增加 400 元,若今年 4 月份与去年4 月份卖出的 A 型车数量相同,则今年 4 月份 A 型车销售总额将比去年 4 月份销售总额增加 25%.(A、B 两种型号车 今年的进货和销售价格如下表所示)
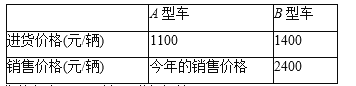
(1)求今年 4 月份 A 型车每辆销售价多少元(用列方程进行解答);
(2)该车行计划 5 月份新进一批 A 型车和 B 型车共 50 辆,设购进的 A 型车为 x 辆,获得的总利润为 y 元,请写 出 y 与 x 之间的函数关系式;
(3)在(2)的条件下,若 B 型车的进货数量不超过 A 型车数量的两倍,应如何进货才能使这批车获利最大?最大 利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
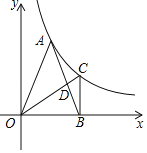
【题目】如图,A为反比例函数y=![]() (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2
(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2![]() .
.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=![]() (x>0)的图象于点C.
(x>0)的图象于点C.
①连接AC,求△ABC的面积;
②在图上连接OC交AB于点D,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
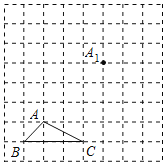
【题目】如图,正方形网格中,小正方形的边长为1.△ABC的顶点都在格点上.
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1逆时针旋转90°,在网格中画出旋转后的△A1B2C2;
(3)在(2)的条件下,直接写出点C1至点C2的经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com