
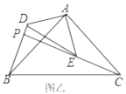
【题目】如图乙,![]() 和
和![]() 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
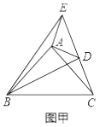
(1)如图甲,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 、
、![]() 、
、![]() 在同一条直线上时,连接
在同一条直线上时,连接![]() 、
、![]() ,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
(2)若![]() ,
,![]() ,把
,把![]() 绕点
绕点![]() 旋转.
旋转.
①当![]() 时,求
时,求![]() 的长;
的长;
②直接写出旋转过程中线段![]() 的最大值和最小值.
的最大值和最小值.
【答案】(1)①②③;(2)①![]() 或
或![]() ;②
;②![]() 长的最小值是
长的最小值是![]() ,最大值是
,最大值是![]() .
.
【解析】
(1)①由条件证明△ABD≌△ACE,就可以得到结论②由△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出∠BDC=90°,进而得出结论;③由条件知∠ABC=∠ABD+∠DBC=45°,由∠ABD=∠ACE就可以得出结论;④△BDE为直角三角形就可以得出BE2=BD2+DE2,由△DAE和△BAC是等腰直角三角形就有DE2=2AD2,BC2=2AB2,就有BC2=BD2+CD2≠BD2就可以得出结论.
(2)①分两种情形a、如图2中,当点E在AB上时,BE=AB-AE=3,由△PEB∽△AEC,得![]() ,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=9,解法类似;
,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=9,解法类似;
②a、如图4中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.b、如图5中,以A为圆心AD为半径画圆,当CE在⊙A下方与⊙A相切时,PB的值最小,分别求出PB即可.
(1)解:如图甲: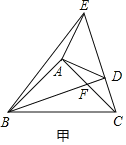
①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
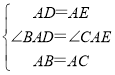 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∴①正确;
②∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠CAB=90°,
∴∠ABD+∠AFB=90°,
∴∠ACE+∠AFB=90°.
∵∠DFC=∠AFB,
∴∠ACE+∠DFC=90°,
∴∠FDC=90°.
∴BD⊥CE,∴②正确;
③∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ABD+∠DBC=45°.
∴∠ACE+∠DBC=45°,∴③正确;
④∵BD⊥CE,
∴BE2=BD2+DE2,
∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴DE2=2AD2,BC2=2AB2,
∵BC2=BD2+CD2≠BD2,
∴2AB2=BD2+CD2≠BD2,
∴BE2≠2(AD2+AB2),∴④错误.
故答案为①②③.
(2)①解:a.如图2中,当点![]() 在
在![]() 上时,
上时,![]() .
.
∵![]() ,
,
∴![]() ,
,
同(1)可证![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
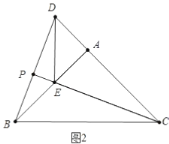
b.如图3中,当点![]() 在
在![]() 延长线上时,
延长线上时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
同(1)可证![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,综上,
,综上,![]() 或
或![]() ;
;
②解:a.如图4中,以![]() 为圆心
为圆心![]() 为半径画圆,当
为半径画圆,当![]() 在
在![]() 下方与
下方与![]() 相切时,
相切时,![]() 的值最小.
的值最小.
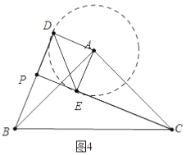
理由:此时![]() 最小,由(1)可知
最小,由(1)可知![]() 是直角三角形,斜边
是直角三角形,斜边![]() 为定值,
为定值,![]() 最小,因此
最小,因此![]() 最小,
最小,
∵![]() ,
,
∴![]() ,
,
由(1)可知,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,且AD=AE=3,
,且AD=AE=3,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ;
;
b.如图5中,以![]() 为圆心
为圆心![]() 为半径画圆,当
为半径画圆,当![]() 在
在![]() 上方与
上方与![]() 相切时,
相切时,![]() 的值最大.
的值最大.
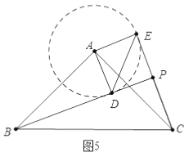
理由:此时![]() 最大,因此
最大,因此![]() 最大,(同理,
最大,(同理,![]() 是直角三角形,斜边
是直角三角形,斜边![]() 为定值,
为定值,![]() 最大,因此
最大,因此![]() 最大)
最大)
∵![]() ,
,
∴![]() ,
,
由(1)可知,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,且AD=AE=3,
,且AD=AE=3,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() .
.
综上所述,![]() 长的最小值是
长的最小值是![]() ,最大值是
,最大值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() 与x轴、y轴分别交于点B,C,抛物线y=
与x轴、y轴分别交于点B,C,抛物线y=![]() 过B,C两点,且与x轴的另一个交点为点A,连接AC.
过B,C两点,且与x轴的另一个交点为点A,连接AC.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点D(与点A不重合),使得S△DBC=S△ABC,若存在,求出点D的坐标;若不存在,请说明理由;
(3)有宽度为2,长度足够长的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线CB于点M和点N,在矩形平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C做⊙O 的切线,与AE的延长线交于点D,且AD⊥CD.
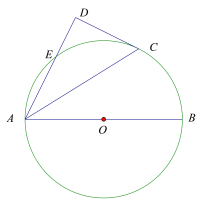
(1)求证:AC平分∠DAB;
(2)若AB=10,CD=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点,设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为_____.
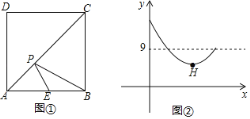
查看答案和解析>>
科目:初中数学 来源: 题型:
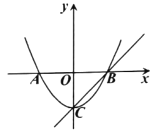
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求二次函数![]() 的解析式;
的解析式;
(3)作直线![]() ,问抛物线
,问抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .若存在,求出点
.若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
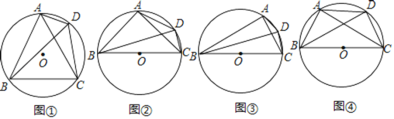
【题目】(1)方法选择:如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.
小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…
小军认为可用补短法证明:延长CD至点N,使得DN=AD…
请你选择一种方法证明.
(2)类比探究:(探究1)如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,井证明你的结论.
(探究2)如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是 .
(3)拓展猜想:如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com