
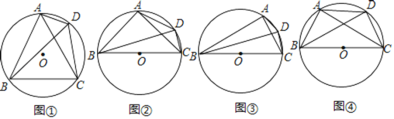
【题目】(1)方法选择:如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.
小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…
小军认为可用补短法证明:延长CD至点N,使得DN=AD…
请你选择一种方法证明.
(2)类比探究:(探究1)如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,井证明你的结论.
(探究2)如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是 .
(3)拓展猜想:如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是 .
【答案】(1)选截长法,见解析;(2)探究1 :BD=CD+![]() AD,见解析;探究2: BD=
AD,见解析;探究2: BD=![]() CD+2AD;(3)BD=
CD+2AD;(3)BD=![]() CD+
CD+![]() AD.
AD.
【解析】
(1)方法选择:根据等边三角形的性质得到∠ACB=∠ABC=60°,如图①,在BD上截取DM=AD,连接AM,由圆周角定理得到∠ADB=∠ACB=60°,得到AM=AD,根据全等三角形的性质得到BM=CD,于是得到结论;
(2)类比探究:探究1:如图②,由BC是⊙O的直径,得到∠BAC=90°,根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,过A作AM⊥AD交BD于M,推出△ADM是等腰直角三角形,求得DM=![]() AD根据全等三角形的性质得到结论;
AD根据全等三角形的性质得到结论;
探究2:如图③,根据圆周角定理和三角形的内角和得到∠BAC=90°,∠ACB=60°,过A作AM⊥AD交BD于M,求得∠AMD=30°,根据直角三角形的性质得到MD=2AD,根据相似三角形的性质得到BM=![]() CD,于是得到结论;
CD,于是得到结论;
(3)如图④,由BC是⊙O的直径,得到∠BAC=90°,过A作AM⊥AD交BD于M,求得∠MAD=90°,根据相似三角形的性质得到BM=![]() CD,DM=
CD,DM=![]() AD,于是得到结论.
AD,于是得到结论.
(1)方法选择:∵AB=BC=AC,
∴∠ACB=∠ABC=60°,
如图①,在BD上截取DM=AD,连接AM,
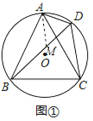
∵∠ADB=∠ACB=60°,
∴△ADM是等边三角形,
∴AM=AD,
∵∠ABM=∠ACD,
∵∠AMB=∠ADC=120°,
∴△ABM≌△ACD(AAS),
∴BM=CD,
∴BD=BM+DM=CD+AD;
(2)类比探究:探究1:如图②,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵AB=AC,
∴∠ABC=∠ACB=45°,
过A作AM⊥AD交BD于M,
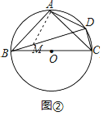
∵∠ADB=∠ACB=45°,
∴△ADM是等腰直角三角形,
∴AM=AD,∠AMD=45°,
∴DM=![]() AD,
AD,
∴∠AMB=∠ADC=135°,
∵∠ABM=∠ACD,
∴△ABM≌△ACD(AAS),
∴BM=CD,
∴BD=BM+DM=CD+![]() AD;
AD;
探究2:如图③,
∵若BC是⊙O的直径,∠ABC=30°,
∴∠BAC=90°,∠ACB=60°,
过A作AM⊥AD交BD于M,
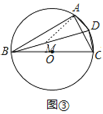
∵∠ADB=∠ACB=60°,
∴∠AMD=30°,
∴MD=2AD,
∵∠ABD=∠ACD,∠AMB=∠ADC=150°,
∴△ABM∽△ACD,
∴![]() ,
,
∴BM=![]() CD,
CD,
∴BD=BM+DM=![]() CD+2AD;
CD+2AD;
故答案为:BD=![]() CD+2AD;
CD+2AD;
(3)拓展猜想:BD=BM+DM=![]() CD+
CD+![]() AD;
AD;
理由:如图④,
∵若BC是⊙O的直径,
∴∠BAC=90°,
过A作AM⊥AD交BD于M,

∴∠MAD=90°,
∴∠BAM=∠DAC,
∴△ABM∽△ACD,
∴![]() ,
,
∴BM=![]() CD,
CD,
∵∠ADB=∠ACB,∠BAC=∠NAD=90°,
∴△ADM∽△ACB,
∴![]() ,
,
∴DM=![]() AD,
AD,
∴BD=BM+DM=![]() CD+
CD+![]() AD.
AD.
故答案为:BD=BM+DM=![]() CD+
CD+![]() AD.
AD.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
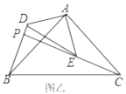
【题目】如图乙,![]() 和
和![]() 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
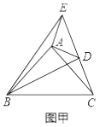
(1)如图甲,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 、
、![]() 、
、![]() 在同一条直线上时,连接
在同一条直线上时,连接![]() 、
、![]() ,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
(2)若![]() ,
,![]() ,把
,把![]() 绕点
绕点![]() 旋转.
旋转.
①当![]() 时,求
时,求![]() 的长;
的长;
②直接写出旋转过程中线段![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(动手操作)
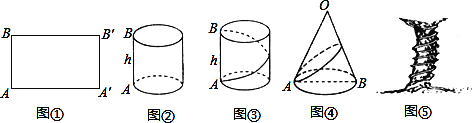
如图①,把长为l、宽为h的矩形卷成以AB为高的圆柱形,则点A′与点______重合,点B′与点______重合;
(探究发现)
如图②,圆柱的底面周长是80,高是60,若在圆柱体的侧面绕一圈丝线作装饰,从下底面A出发,沿圆柱侧面绕一周到上底面B,则这条丝线最短的长度是______;
(实践应用)
如图③,圆锥的母线长为12,底面半径为4,若在圆锥体的侧面绕一圈彩带做装饰,从圆锥的底面上的点A出发,沿圆锥侧面绕一周回到点A.求这条彩带最短的长度是多少?
(拓展联想)
如图④,一颗古树上下粗细相差不大,可以看成圆柱体.测得树干的周长为3米,高为18米,有一根紫藤自树底部均匀的盘绕在树干上,恰好绕8周到达树干的顶部,这条紫藤至少有 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
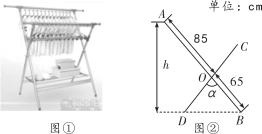
【题目】有一种落地晾衣架如图①所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图②是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85 cm,BO=DO=65 cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为______cm.(参考数据:sin 37°≈0.6,cos 37°≈0.8,sin 53°≈0.8,cos 53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
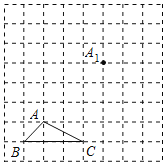
【题目】如图,正方形网格中,小正方形的边长为1.△ABC的顶点都在格点上.
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1逆时针旋转90°,在网格中画出旋转后的△A1B2C2;
(3)在(2)的条件下,直接写出点C1至点C2的经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
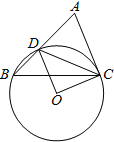
【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.如果∠ACB=75°,圆O的半径为2,则BD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:对于关于![]() 的函数
的函数![]() 我们称函数
我们称函数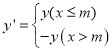 为函数
为函数![]() 的
的![]() 分函数(其中
分函数(其中![]() 为常数).
为常数).
例如:对于关于![]() 的一次函数
的一次函数![]() 的
的![]() 分函数为
分函数为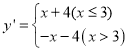
(1)若点![]() 在关于
在关于![]() 的一次函数
的一次函数![]() 的
的![]() 分函数上,求
分函数上,求![]() 的值.
的值.
(2)写出反比例函数![]() 的
的![]() 分函数的图象上
分函数的图象上![]() 随
随![]() 的增大而减小的
的增大而减小的![]() 的取值范围 ;
的取值范围 ;
(3)若![]() 是二次函数
是二次函数![]() 关于
关于![]() 的
的![]() 分函数.
分函数.
![]() 当
当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
![]() 当
当![]() 时,
时,![]() 则
则![]() 的取值范围为 ;
的取值范围为 ;
(4)若点![]() 连结
连结![]() 当关于
当关于![]() 的二次函数
的二次函数![]() 的
的![]() 分函数,与线段
分函数,与线段![]() 有两个交点,直接写出
有两个交点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
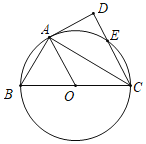
【题目】如图,已知BC是⊙O的直径,AD切⊙于点A,CD∥OA交⊙O于另一点E.
(1)求证:△ACD∽△BCA;
(2)若A是⊙O上一动点,则
①当∠B=_____时,以A,O,C,D为顶点的四边形是正方形;
②当∠B=_____时,以A,O,C,E为顶点的四边形是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com