
����Ŀ�������ֲ�����
��ͼ�����ѳ�Ϊl����Ϊh�ľ��ξ�����ABΪ�ߵ�Բ���Σ����A�����______�غϣ���B�����______�غϣ�
��̽�����֣�
��ͼ����Բ���ĵ����ܳ���80������60������Բ����IJ�����һȦ˿����װ�Σ����µ���A��������Բ��������һ�ܵ��ϵ���B��������˿����̵ij�����______��
��ʵ��Ӧ�ã�
��ͼ����Բ��ĸ�߳�Ϊ12������뾶Ϊ4������Բ��IJ�����һȦ�ʴ���װ�Σ���Բ�ĵ����ϵĵ�A��������Բ������һ�ܻص���A���������ʴ���̵ij����Ƕ��٣�
����չ���룩
��ͼ����һ�Ź������´�ϸ�����Կ���Բ���壮������ɵ��ܳ�Ϊ3�ף���Ϊ18�ף���һ�����������ײ����ȵ������������ϣ�ǡ����8�ܵ������ɵĶ������������������� ��
���𰸡������ֲ�������A��B����̽�����֡�100 ����ʵ��Ӧ�á���![]() ������չ���롿30
������չ���롿30
��������
[���ֲ���]����Բ���IJ���չ��ͼ�Ǿ��μ��ɵõ��𰸣�
[̽������] ����![]() �����ݾ��ε����ʼ����ɶ������
�����ݾ��ε����ʼ����ɶ������![]() ���ɵõ��𰸣�
���ɵõ��𰸣�
[ʵ��Ӧ��]��Բչ���õ�չ��ͼ������![]() �����ݻ�����ʽ�����
�����ݻ�����ʽ�����![]() �Ķ���������O��OD��
�Ķ���������O��OD��![]() �ڵ�D�����ݵ��������ε����ʼ�ֱ�������ε��������OD=6�������ù��ɶ������AD���ɵõ��𰸣�
�ڵ�D�����ݵ��������ε����ʼ�ֱ�������ε��������OD=6�������ù��ɶ������AD���ɵõ��𰸣�
[��չ����]�����ɵĸ߶ȷֳ���ȵ�8�Σ��������ɵ��ܳ��������ɶ����ĵ�ʽ���һȦ���ٵij����ɴ˵õ���.
[���ֲ���]��![]() ���A�غϣ���
���A�غϣ���![]() ���B�غϣ�
���B�غϣ�
�ʴ�Ϊ��A��B��
[̽������]������֪��Բ���IJ���չ��ͼ���Ǿ���![]() ����
����![]() =80��
=80��![]() =60��
=60��
����![]() ��
��
�ߡ�![]() =90����
=90����
��![]() ,
,
������˿����̵ij�����100��
�ʴ�Ϊ��100��
[ʵ��Ӧ��]
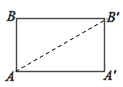
�⣺Բ�IJ���չ��ͼ����ͼ��ʾ��
����![]() ��
��
��![]() Ϊ���·����
Ϊ���·����
��![]() �ij���
�ij���![]() ��
��
�ɻ�����ʽ����![]() �Ķ���Ϊ��
�Ķ���Ϊ��![]()
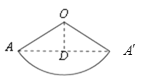
����O��OD��![]() �ڵ�D��
�ڵ�D��
���AOD=60����
����OAD=30����
��OD=6��
��Rt��AOD��![]() ��
��
�������ʴ���̵ij�����![]() ��
��
[��չ����]�����ɵĸ���18�ף�����8Ȧ���٣�
��ÿ������Ȧ���ٵľ�����![]() �ף�
�ף�
�����ɵ��ܳ���3�ף�
��һȦ���ٵij�����![]() �ף�
�ף�
��8Ȧ���ٵij���������![]() �ף�
�ף�
�ʴ�Ϊ��30.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��������ABC�Ƶ�C˳ʱ����ת180���õ���EFC������AF��BE��
��1����֤���ı���ABEF��ƽ���ı��Σ�
��2������ABCΪ���ٶ�ʱ���ı���ABEFΪ���Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
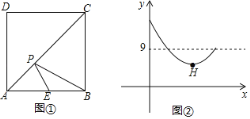
����Ŀ����ͼ������������ABCD�У���E��AB���е㣬��P�ǶԽ���AC��һ���㣬��PC�ij���Ϊx��PE��PB�ij��Ⱥ�Ϊy��ͼ����y����x�ĺ���ͼ����ͼ������͵�H������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
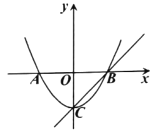
����Ŀ����ͼ����֪����Ϊ![]() ��������
��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
��2������κ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��3����ֱ��![]() ����������
����������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����꣺�������ڣ���˵�����ɣ�
�����꣺�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
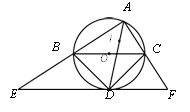
����Ŀ����ͼ��A����BCΪֱ������O��һ�㣬I����ABC�����ģ�AI���ӳ��߽���O�ڵ�D������D��BC��ƽ���߽�AB��AC���ӳ�����E��F������˵�����١�DBC�ǵ���ֱ�������Σ���EF����O���У���EF=2BC������B��I��C���Ե�D ΪԲ�ĵ�ͬһ��Բ�ϣ�����һ����ȷ����_______��������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��D��ͬһ��ֱ���ϣ���E��F�ֱ���ֱ��AD�����࣬��AE=DF����A=��D��AB=DC��
��1����֤���ı���BFCE��ƽ���ı��Σ�
��2����AD=10��DC=3����EBD=60������BE= ʱ���ı���BFCE�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��![]() ��a��
��a��![]() ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������

A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
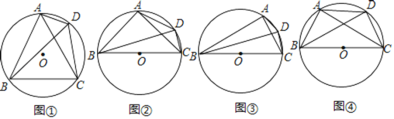
����Ŀ����1������ѡ����ͼ�٣��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD��AB��BC��AC����֤��BD��AD+CD��
Сӱ��Ϊ���ýس���֤������DB�Ͻ�ȡDM��AD������AM��
С����Ϊ���ò��̷�֤�����ӳ�CD����N��ʹ��DN��AD��
����ѡ��һ�ַ���֤����
��2�����̽������̽��1����ͼ�ڣ��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD��BC�ǡ�O��ֱ����AB��AC�����õ�ʽ��ʾ�߶�AD��BD��CD֮���������ϵ����֤����Ľ��ۣ�
��̽��2����ͼ�ۣ��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD����BC�ǡ�O��ֱ������ABC��30�������߶�AD��BD��CD֮��ĵ�����ϵʽ���� ����
��3����չ���룺��ͼ�ܣ��ı���ABCD�ǡ�O���ڽ��ı��Σ�����AC��BD����BC�ǡ�O��ֱ����BC��AC��AB��a��b��c�����߶�AD��BD��CD֮��ĵ�����ϵʽ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����2m+1��x+m2��4=0����������ȵ�ʵ����
��1����ʵ��m��ȡֵ��Χ��
��2��������ʵ������ƽ���͵���15����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com