
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于![]() BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
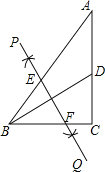
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),以
重合),以![]() 长为半径的
长为半径的![]() 与边
与边![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
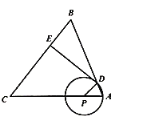
![]() 当
当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的半径;
的半径;
![]() 联结
联结![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围;
的取值范围;
![]() 在
在![]() 的条件下,当以
的条件下,当以![]() 长为直径的
长为直径的![]() 与
与![]() 相交于
相交于![]() 边上的点
边上的点![]() 时,求相交所得的公共弦的长.
时,求相交所得的公共弦的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
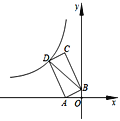
【题目】如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线![]() (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
(k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题:
探究:(1)若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是 ;如图2,当a= °时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:(3)如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;
cosα= (用含有R、m的代数式表示)
拓展:(4)如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 ,并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次聚会上,规定每两个人见面必须握手,且握手1次.
(1)若参加聚会的人数为3,则共握手 次;若参加聚会的人数为5,则共握手 次;
(2)若参加聚会的人数为n(n为正整数),则共握手 次;
(3)若参加聚会的人共握手28次,请求出参加聚会的人数.
(4)嘉嘉由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A,B),线段总数为多少呢?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一棵古树![]() 和教学楼
和教学楼![]() 的高,先在
的高,先在![]() 处用高1.5米的测角仪测得古树顶端
处用高1.5米的测角仪测得古树顶端![]() 的仰角
的仰角![]() 为
为![]() ,此时教学楼顶端
,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走9米到达
上,再向前走9米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为
为![]() ,点
,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
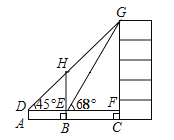
(1)计算古树![]() 的高;
的高;
(2)计算教学楼![]() 的高.(结果精确到0.1米,参考数据:
的高.(结果精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
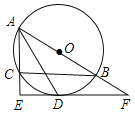
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 是
是![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 的切线,连接
的切线,连接![]() 并延长,交过点
并延长,交过点![]() 的切线于点
的切线于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
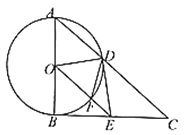
(1)求证:![]() 是
是![]() 切线;
切线;
(2)当![]() _______度时,四边形
_______度时,四边形![]() 为正方形;
为正方形;
(3)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() _______时,四边形
_______时,四边形![]() 为菱形.
为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com