
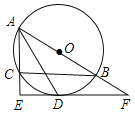
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,由OA=OD知∠OAD=∠ODA,由AD平分∠EAF知∠DAE=∠DAO,据此可得∠DAE=∠ADO,继而知OD∥AE,根据AE⊥EF即可得证;
(2)作OG⊥AE,知AG=CG=![]() AC=2,证四边形ODEG是矩形得OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=48,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
AC=2,证四边形ODEG是矩形得OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=48,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
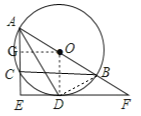
(1)如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠EAF,
∴∠DAE=∠DAO,
∴∠DAE=∠ADO,
∴OD∥AE,
∵AE⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)如图,作OG⊥AE于点G,连接BD,
则AG=CG=![]() AC=2,∠OGE=∠E=∠ODE=90°,
AC=2,∠OGE=∠E=∠ODE=90°,
∴四边形ODEG是矩形,
∴OA=OB=OD=CG+CE=2+2=4,∠DOG=90°,
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD,
∴![]() ,即
,即![]() ,
,
∴AD2=48,
在Rt△ABD中,BD=![]() =4,
=4,
在Rt△ABD中,∵AB=2BD,
∴∠BAD=30°,
∴∠BOD=60°,
则![]() 的长度为
的长度为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
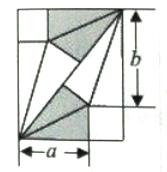
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若![]() ,
,![]() ,则该长方形的面积为__________.
,则该长方形的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
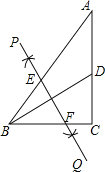
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于![]() BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
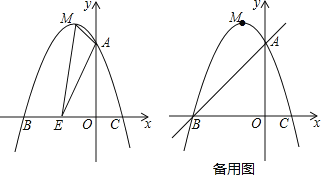
【题目】如图,抛物线y=ax2+bx+3交y轴于点A,交x轴于点B(-3,0)和点C(1,0),顶点为点M.
(1)求抛物线的解析式;
(2)如图,点E为x轴上一动点,若△AME的周长最小,请求出点E的坐标;
(3)点F为直线AB上一个动点,点P为抛物线上一个动点,若△BFP为等腰直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为﹣2;④使y≤3成立的x的取值范围是x≥0;⑤抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<﹣1<x2,且x1+x2>﹣2,则y1<y2其中正确的个数有( )
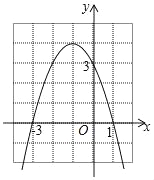
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为![]() 元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于
元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数
(元/件)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)写出销售单价![]() 的取值范围;
的取值范围;
(2)求出一次函数![]() 的解析式;
的解析式;
(3)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
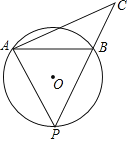
【题目】如图,在半径为5的⊙O中,弦AB=6,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批A、B两型号节能灯,已知2只A型节能灯和3只B型节能灯共需31元;1只A型节能灯和2只B型节能灯共需19元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共100只,并且A型节能灯的数量不多于B型节能灯数量的2倍,请设计出最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com