
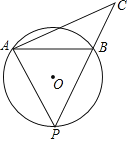
【题目】如图,在半径为5的⊙O中,弦AB=6,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为____.
【答案】6或![]() 或
或![]()
【解析】
由于本题的等腰三角形的底和腰不确定,分三种情况讨论:
①当BA=BP时,利用直角三角形斜边的中线等于斜边的一半;
②当AB=AP时,连接AO交PB于点D,过点O作OE⊥AB于点E,易得△AOE∽△ABD,利用相似三角形的性质求得BD,PB,然后利用相似三角形的判定定理△ABD∽△CPA,代入数据得出结果;
③当PA=PB时,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,则PF⊥AB,易得AF=FB=3,利用勾股定理得OF=4,FP=9,易得△PFB∽△CGB,利用相似三角形的性质可求出CG:BG的值,设BG=t,则CG=3t,利用相似三角形的判定定理得△APF∽△CAG,利用相似三角形的性质得比例关系解得t,在Rt△BCG中,由勾股定理得出BC的长.
①当BA=BP时,
则AB=BP=BC=6,即线段BC的长为6;
②当AB=AP时,如图1,连接AO交PB于点D,过点O作OE⊥AB于点E,则AD⊥PB,AE=![]() AB=3,
AB=3,

∴BD=DP,
在Rt△AEO中,AE=3,AO=5,
∴OE=![]() =4,
=4,
∵∠OAE=∠BAD,∠AEO=∠ADB=90°,
∴△AOE∽△ABD,
∴![]() ,即
,即![]() ,
,
∴BD=![]() ,
,
∴BD=PD=![]() ,即PB=
,即PB=![]() ,
,
∵AB=AP=6,
∴∠ABD=∠APC,
∵∠PAC=∠ADB=90°,
∴△ABD∽△CPA,
∴![]() ,即
,即![]() ,
,
∴CP=![]() ,
,
∴BC=BP-CP=![]() -
-![]() =
=![]() ;
;
③当PA=PB时,
如图2,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,则PF⊥AB,
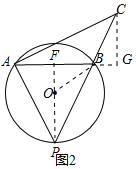
∴AF=FB=3,
在Rt△OFB中,OB=5,FB=3,∴OF=4,
∴FP=9,
∵∠PAF=∠ABP=∠CBG,∠AFP=∠CGB=90°,
∴△PFB∽△CGB,
∴![]() ,
,
设BG=t,则CG=3t,
∵∠PAF=∠ACG,∠AFP=∠AGC=90°,
∴△APF∽△CAG,
∴![]() ,
,
∴![]() ,
,
解得t=![]() ,
,
∴BG=![]() ,CG=
,CG=![]() ,
,
在Rt△BCG中,BC=![]() ,
,
综上所述,当△PAB是等腰三角形时,线段BC的长为6或![]() 或
或![]() ;
;
故答案为:6或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
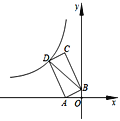
【题目】如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线![]() (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
(k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
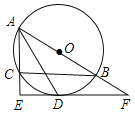
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
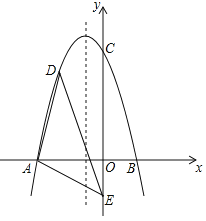
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
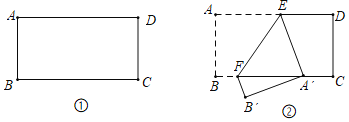
【题目】如图①,在矩形纸片ABCD中,AB=4,AD=6.点E,F分别在AB,DC上(E不与A,D重合,F不与B,C重合),现以EF为折痕,将矩形纸片ABCD折叠.
(1)当A点落在BC上时(如图②),求证:△EFA′是等腰三角形;
(2)当A′点与C重合时,试求△EFA’的面积;
(3)当A′点与DC的中点重合时,试求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |


(1)写出运动员甲测试成绩的众数为_____;运动员乙测试成绩的中位数为_____;运动员丙测试成绩的平均数为_____;
(2)经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 是
是![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 的切线,连接
的切线,连接![]() 并延长,交过点
并延长,交过点![]() 的切线于点
的切线于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
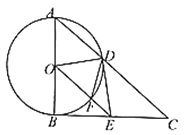
(1)求证:![]() 是
是![]() 切线;
切线;
(2)当![]() _______度时,四边形
_______度时,四边形![]() 为正方形;
为正方形;
(3)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() _______时,四边形
_______时,四边形![]() 为菱形.
为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com