
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),以
重合),以![]() 长为半径的
长为半径的![]() 与边
与边![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
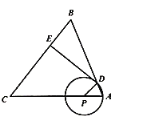
![]() 当
当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的半径;
的半径;
![]() 联结
联结![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围;
的取值范围;
![]() 在
在![]() 的条件下,当以
的条件下,当以![]() 长为直径的
长为直径的![]() 与
与![]() 相交于
相交于![]() 边上的点
边上的点![]() 时,求相交所得的公共弦的长.
时,求相交所得的公共弦的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=![]() ,则sinC=
,则sinC=![]() ,sinC=
,sinC=![]() =
=![]() =
=![]() ,即可求解;
,即可求解;
(2)PD∥BE,则![]() =
=![]() ,即:
,即:![]() ,即可求解;
,即可求解;
(3)证明四边形PDBE为平行四边形,则AG=GP=BD,即:AB=DB+AD=AG+AD=4![]() ,即可求解.
,即可求解.
(1)设⊙P与边BC相切的切点为H,圆的半径为R,
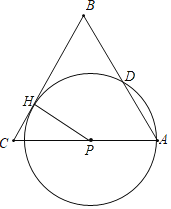
连接HP,则HP⊥BC,cosC=![]() ,则sinC=
,则sinC=![]() ,
,
sinC=![]() =
=![]() =
=![]() ,解得:R=
,解得:R=![]() ;
;
(2)在△ABC中,AC=BC=10,cosC=![]() ,
,
设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,
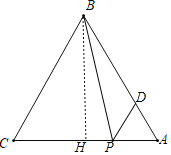
则BH=ACsinC=8,
同理可得:
CH=6,HA=4,AB=4![]() ,则:tan∠CAB=2BP=
,则:tan∠CAB=2BP=![]() =
=![]() ,
,
DA=![]() x,则BD=4
x,则BD=4![]() -
-![]() x,
x,
如下图所示,

PA=PD,∴∠PAD=∠CAB=∠CBA=β,
tanβ=2,则cosβ=![]() ,sinβ=
,sinβ=![]() ,
,
EB=BDcosβ=(4![]() -
-![]() x)×
x)×![]() =4-
=4-![]() x,
x,
∴PD∥BE,
∴![]() =
=![]() ,即:
,即:![]() ,
,
整理得:y=![]() ;
;
(3)以EP为直径作圆Q如下图所示,
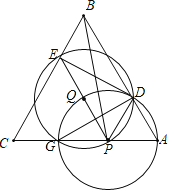
两个圆交于点G,则PG=PQ,即两个圆的半径相等,则两圆另外一个交点为D,GD为相交所得的公共弦,
∵点Q时弧GD的中点,
∴DG⊥EP,
∵AG是圆P的直径,
∴∠GDA=90°,
∴EP∥BD,
由(2)知,PD∥BC,∴四边形PDBE为平行四边形,
∴AG=EP=BD,
∴AB=DB+AD=AG+AD=4![]() ,
,
设圆的半径为r,在△ADG中,
AD=2rcosβ=![]() ,DG=
,DG=![]() ,AG=2r,
,AG=2r,
![]() +2r=4
+2r=4![]() ,解得:2r=
,解得:2r=![]() ,
,
则:DG=![]() =10-2
=10-2![]() ,
,
相交所得的公共弦的长为10-2![]() .
.


科目:初中数学 来源: 题型:
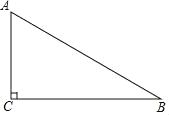
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连接AP,若AP平分∠CAB,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把正![]() 边形(
边形(![]() )的各边三等分,分别以居中的那条线段为一边向外作正
)的各边三等分,分别以居中的那条线段为一边向外作正![]() 边形,并去掉居中的那条线段,得到一个新的图形叫做正
边形,并去掉居中的那条线段,得到一个新的图形叫做正![]() 边形的“扩展图形”,并将它的边数记为
边形的“扩展图形”,并将它的边数记为![]() ,如图
,如图![]() ,将正三角形进行上述操作后得到其“扩展图形”,且
,将正三角形进行上述操作后得到其“扩展图形”,且![]() .图
.图![]() 、图
、图![]() 分别是正五边形、正六边形的“扩展图形”。
分别是正五边形、正六边形的“扩展图形”。
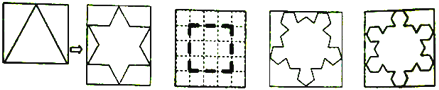
(1)如图![]() ,在
,在![]() 的正方形网格中用较粗的虚线画有一个正方形,请在图
的正方形网格中用较粗的虚线画有一个正方形,请在图![]() 中用实线画出此正方形的“扩展图形”;
中用实线画出此正方形的“扩展图形”;
(2)已知![]() ,则图
,则图![]() 中
中![]() =_____,根据以上规律,正
=_____,根据以上规律,正![]() 边形的“扩展图形”的
边形的“扩展图形”的![]() =______;(用含
=______;(用含![]() 的式子表示)
的式子表示)
(3)已知![]() ,且
,且![]() ,则
,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
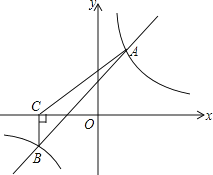
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A(2,3),B(-3,m)两点.
(m≠0)的图象相交于A(2,3),B(-3,m)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为点C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则![]() 的长为______(用含n,π的式子表示).
的长为______(用含n,π的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
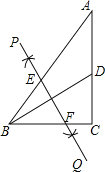
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于![]() BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com