
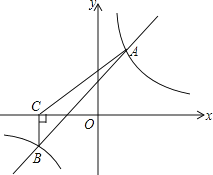
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A(2,3),B(-3,m)两点.
(m≠0)的图象相交于A(2,3),B(-3,m)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为点C,求S△ABC.
【答案】(1)反比例函数解析式为y=![]() ,一次函数解析式为y=x+1;(2)-3<x<0或x>2;(3)5.
,一次函数解析式为y=x+1;(2)-3<x<0或x>2;(3)5.
【解析】
(1)先把A点坐标代入y=![]() 可求出n的值,从而确定反比例函数解析式;再把B(-3,m)代入反比例函数解析式求出m的值,然后利用待定系数法求一次函数解析式;
可求出n的值,从而确定反比例函数解析式;再把B(-3,m)代入反比例函数解析式求出m的值,然后利用待定系数法求一次函数解析式;
(2)观察函数图象得到,当-3<x<0或x>2时,一次函数图象在反比例函数图象上方;
(3)先确定直线y=x+1与x轴交点D的坐标和C点坐标,然后利用S△ABC=S△DBC+S△ADC进行计算.
(1)把A(2,3)代入y=![]() 得n=2×3=6,
得n=2×3=6,
所以反比例函数解析式为y=![]() ,
,
把B(-3,m)代入y=![]() 得-3m=6,解得m=-2,则B点坐标为(-3,-2),
得-3m=6,解得m=-2,则B点坐标为(-3,-2),
把A(2,3)、B(-3,-2)代入y=kx+b得
![]() ,解得
,解得![]() ,
,
所以一次函数解析式为y=x+1;
(2)不等式kx+b>![]() 的解集为-3<x<0或x>2;
的解集为-3<x<0或x>2;
(3)如图,直线y=x+1与x轴交点为D,则D(-1,0),
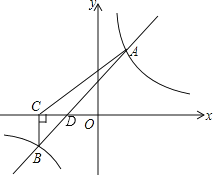
因为BC⊥x轴,
所以C点坐标为(-3,0),
所以S△ABC=S△DBC+S△ADC=![]() ×2×2+
×2×2+![]() ×2×3=5.
×2×3=5.


科目:初中数学 来源: 题型:
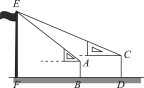
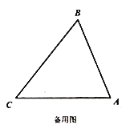
【题目】某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在D点测得旗杆顶端E点的仰角为30°.已知小明和小军的距离BD=6 m,小明的身高AB=1.5 m,小军的身高CD=1.75 m,求旗杆的高EF.(结果精确到0.1,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=![]() (x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
(x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
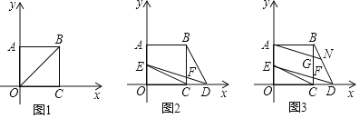
【题目】如图,矩形ABCO在平面直角坐标系中,AO,CO分别在y轴,x轴正半轴上,若S矩形AOCB=![]() BO2,矩形AOCB的周长为16.
BO2,矩形AOCB的周长为16.
(1)求B点坐标;
(2)点D在OC延长线上,设D点横坐标为d,连BD,将直线DB绕D点逆时针方向旋转45°交AO于E,交BC于F,连EC,设△CDE面积=S,求出S与d的函数关系式并注明自变量d的取值范围;
(3)在(2)条件下,当点E在AO上时,过A作ED的平行线交CB于G,交BD于N,若BG=2CF,求S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),以
重合),以![]() 长为半径的
长为半径的![]() 与边
与边![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
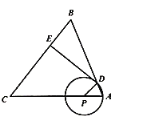
![]() 当
当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的半径;
的半径;
![]() 联结
联结![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围;
的取值范围;
![]() 在
在![]() 的条件下,当以
的条件下,当以![]() 长为直径的
长为直径的![]() 与
与![]() 相交于
相交于![]() 边上的点
边上的点![]() 时,求相交所得的公共弦的长.
时,求相交所得的公共弦的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在多项式的乘法公式中,完全平方公式![]() 是其中重要的一个.
是其中重要的一个.
(1)请补全完全平方公式的推导过程:
![]() ,
,
![]() ,
,
![]() .
.
(2)如图,将边长为![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
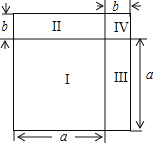
(3)用完全平方公式求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题:
探究:(1)若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是 ;如图2,当a= °时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:(3)如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;
cosα= (用含有R、m的代数式表示)
拓展:(4)如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 ,并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com