练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

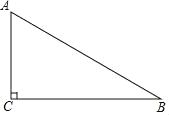
    【题目】如图，在Rt△ABC中，∠ACB＝90°．

    （1）用尺规在边BC上求作一点P，使PA＝PB（不写作法，保留作图痕迹）；

    （2）连接AP，若AP平分∠CAB，求∠B的度数．

    【答案】（1）作图见解析；（2）30°.

    【解析】

    （1）作线段AB的垂直平分线即可；
    （2）根据线段垂直平分线的性质可得BP=AP，根据等边对等角可得∠B=∠PAB，然后再根据角平分线定义可得∠CAP=∠PAB，进而可得∠B=∠PAB=∠CAP，然后可得答案

    解：（1）如图：作线段AB的垂直平分线；

    （2）∵PD是线段AB的垂直平分线，

    ∴PA＝PB，

    ∴∠B＝∠PAB，

    ∵AP平分∠CAB，

    ∴∠CAP＝∠PAB，

    ∴∠B＝∠PAB＝∠CAP，

    ∵∠ACB＝90°，

    ∴∠B＝∠PAB+∠CAP＝90°，

    ∴∠B＝30°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB于点，连结OE，AC，且∠P=∠E，∠POE=2∠CAB．

    （1）求证：CE⊥AB；

    （2）求证：PC是⊙O的切线；

    （3）若BD=2OD，且PB=9，求⊙O的半径长和tan∠P的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

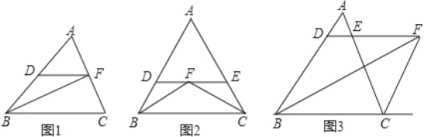
    【题目】（1）如图 1，在△ABC 中，∠ABC 的平分线 BF 交 AC 于 F， 过点 F 作 DF∥BC， 求证：BD=DF．

    （2）如图 2，在△ABC 中，∠ABC 的平分线 BF 与∠ACB 的平分线 CF 相交于 F，过点 F 作 DE∥BC，交直线 AB 于点 D，交直线 AC 于点 E．那么 BD，CE，DE 之间存在什么关系？并证明这种关系．

    （3）如图 3，在△ABC 中，∠ABC 的平分线 BF 与∠ACB 的外角平分线 CF 相交于 F，过点 F 作 DE∥BC，交直线 AB 于点D，交直线 AC 于点 E．那么 BD，CE，DE 之间存在什么关系？请写出你的猜想．（不需证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

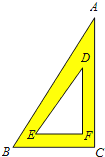
    【题目】一块含30°角的直角三角板（如图），它的斜边AB=8cm，里面空心△DEF的各边与△ABC的对应边平行，且各对应边的距离都是1cm，那么△DEF的周长是（ ）

    A、5cm B、6cm C、（6-）cm D、（3+）cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°，顶部的仰角为37°，已知教学楼和实验楼在同一平面上，观测点距地面的垂直高度AB为15m，求实验楼的垂直高度即CD长（精确到1m）．

    参考值：sin37°=0.60，cos37°=0.80，tan37°=0.75．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“校园安全”受到全社会的广泛关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

    (1)接受问卷调查的学生共有_______人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°；

    (2)请补全条形统计图；

    (3)若该中学共有学生1800人，请根据上述调查结果，估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

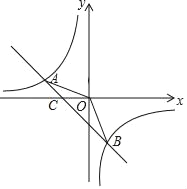
    【题目】已知如图，一次函数y=kx+b的图象与反比例函数y=的图象相交于A、B两点，A点坐标是（﹣2，1），B点坐标（1，n）；

    （1）求出k，b，m，n的值；

    （2）求△AOB的面积；

    （3）直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

    （1）如图 1，在四边形 ABCD 中，添加一个条件使得四边形 ABCD 是“等邻边四边形”．请写出你添加的一个条件．

    （2）小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？请说明理由．

    （3）如图 2，小红作了一个Rt△ABC，其中∠ABC＝90°，AB＝2，BC＝1，并将 Rt△ABC 沿∠ABC 的平分线 BB′方向平移得到△A′B′C′，连结 AA′， BC′．小红要使得平移后的四边形 ABC′A′是“等邻边四边形”，应平移多少距离（即线段 B′B 的长）？

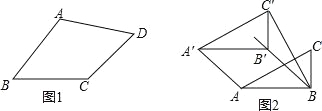
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】市政规划出一块矩形土地用于某项目开发，其中，设计分区如图所示，为矩形内一点，作于点交于点，过点作交于点，其中丙区域用于主建筑区，其余各区域均用于不同种类绿化．

    若点是的中点，求的长；

    要求绿化占地面积不小于，规定乙区域面积为

    ①若将甲区域设计成正方形形状，能否达到设计绿化要求?请说明理由；

    ②若主建筑丙区域不低于乙区域面积的，则的最大值为 （请直接写出答案）

    查看答案和解析>>

    同步练习册答案