
【题目】已知如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
(1)求出k,b,m,n的值;
(2)求△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围.
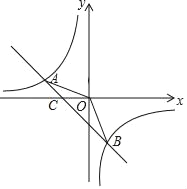
【答案】(1)k=﹣1,b=﹣1,m=﹣2,n=﹣2;(2)S△AOB=![]() ;(3)x<﹣2或0<x<1
;(3)x<﹣2或0<x<1
【解析】
(1)将点A,点B坐标代入两个解析式可求k,b,m,n的值;(2)由题意可求点C坐标,根据△AOB的面积=△ACO面积+△BOC面积,可求△AOB的面积;(3)根据一次函数图象在反比例图象的上方,可求x的取值范围
解:(1)∵反比例函数y=![]() 的图象过点A(﹣2,1),B(1,n)
的图象过点A(﹣2,1),B(1,n)
∴m=﹣2×1=﹣2,m=1×n
∴n=﹣2
∴B(1,﹣2)
∵一次函数y=kx+b的图象过点A,点B
∴![]()
解得:k=﹣1,b=﹣1
∴直线解析式y=﹣x﹣1
(2)∵直线解析式y=﹣x﹣1与x轴交于点C
∴点C(﹣1,0)
∴S△AOB=![]() ×1×1+
×1×1+![]() ×1×2=
×1×2=![]()
(3)由图象可得:x<﹣2或0<x<1


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象经过点(﹣1,﹣2
的图象经过点(﹣1,﹣2![]() ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当![]() 时,则点C的坐标为______.
时,则点C的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
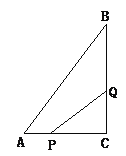
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
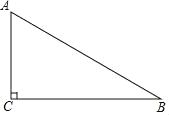
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连接AP,若AP平分∠CAB,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,AB=4,以AB为直径的半圆与BC边交于点D,过点D作DE⊥AC,垂足为E,过点E作EF⊥AB,垂足为F,连接FD.
(1)求证:DE是⊙O的切线;
(2)求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某贮水塔在工作期间,每小时的进水量和出水量都是固定不变的.从凌晨4点到早8点只进水不出水,8点到12点既进水又出水,14点到次日凌晨只出水不进水.下图是某日水塔中贮水量y(立方米)与x(时)的函数图象.
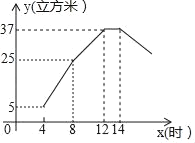
(1)求每小时的进水量;
(2)当8≤x≤12时,求y与x之间的函数关系式;
(3)从该日凌晨4点到次日凌晨,当水塔中的贮水量不小于28立方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
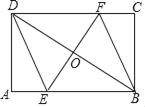
【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线![]() 与直线
与直线![]() 互为“友好直线”,如:直线
互为“友好直线”,如:直线![]() 与
与![]() 互为“友好直线”.
互为“友好直线”.
(1)点![]() 在直线
在直线![]() 的“友好直线”上,则
的“友好直线”上,则![]() ________.
________.
(2)直线![]() 上的点
上的点![]() 又是它的“友好直线”上的点,求点
又是它的“友好直线”上的点,求点![]() 的坐标;
的坐标;
(3)对于直线![]() 上的任意一点
上的任意一点![]() ,都有点
,都有点![]() 在它的“友好直线”上,求直线
在它的“友好直线”上,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com