
【题目】某校2015年八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
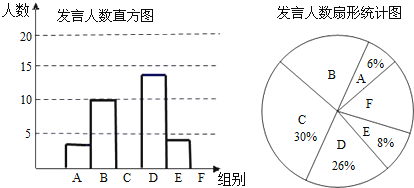
发言次数n | 人数 | 百分比 | |
A | 0≤n<3 | ||
B | 3≤n<6 | ||
C | 6≤n<9 | ||
D | 9≤n<12 | ||
E | 12≤n<15 | ||
F | 15≤n<18 |
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
【答案】(1)50,图形见解析;(2)这天里发言次数不少于12的次数为90次;
(3)概率为![]() .
.
【解析】试题分析:(1)根据B、E两组人数的比例,确定出E组的人数,再根据E组所占的百分比确定样本容量,再求出C、F两组的人数,从而补全直方图;
(2)用总人数乘以E、F两组人数所占的比例即可;
(3)根据题意画出树状图即可求得.
试题解析:(1)∵由发言人数直方图可知B组发言人为10人,又已知B、E两组发言人数的比为5:2, ∴E组发言人为4人
又由发言人数扇形统计图可知E组为8%,∴发言人总数为4÷8%=50人,
于是由扇形统计图知A组、C组、D组分别为3人,15人,13人,
∴F组为50-3-10-15-13-4=5人,于是补全直方图为:
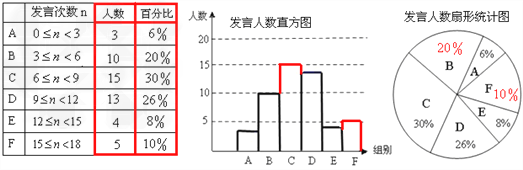
(2) ∵在统计的50人中,发言次数n≥12的有4+5=9人
∴在这天里发言次数不少于12的概率为![]() =18%,
=18%,
∴全年级500人中,在这天里发言次数不少于12的次数为500×18%=90次;
(3)∵A、E组人数分别为3人、4人,又各恰有1女
∴由题意可画树状图为:
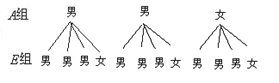
∴由一男一女有5种情况,共有12种情况,于是所抽的两位学生恰好是一男一女的概率为![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
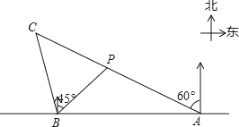
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了解小区500户居民家庭平均月使用塑料袋的数量情况,随机调查了10户居民家庭月使用塑料袋的数量,结果如下(单位:只):65,70,85,74,86,78,74,92,82,94.
根据统计情况,估计该小区这500户家庭每月一共使用塑料袋_________只.
查看答案和解析>>
科目:初中数学 来源: 题型:
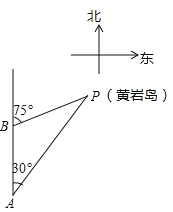
【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: ![]() ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN. 
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,
, ![]() 在数轴上对应的实数分别是
在数轴上对应的实数分别是![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 满足
满足![]() .
.
(![]() )求线段
)求线段![]() 的长.
的长.
(![]() )点
)点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,且
,且![]() 是方程
是方程![]() 的解,在数轴上是否存在点
的解,在数轴上是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 对应的数;若不存在,说明理由.
对应的数;若不存在,说明理由.
(![]() )在(
)在(![]() )和(
)和(![]() )的条件下,点
)的条件下,点![]() ,
, ![]() ,
, ![]() 同时开始在数轴上运动,若点
同时开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度是速度向左运动,点
个单位长度是速度向左运动,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,点
个单位长度的速度向右运动,点![]() 与点
与点![]() 之间距离表示为
之间距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .设运动时间为
.设运动时间为![]() 秒,试探究,随着时间
秒,试探究,随着时间![]() 的变化,
的变化, ![]() 与
与![]() 满足怎样的数量关系?请写出相应的等式.
满足怎样的数量关系?请写出相应的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB:y=﹣ ![]() x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
(1)求A、B两点的坐标;
(2)动点M从A点出发,以每秒1个单位长度的速度,沿x轴向左运动,连接CM.设点M的运动时间为t,△COM的面积为S,求S与t的函数关系式;(并标出自变量的取值范围)
(3)直线AB与直线CM相交于点N,点P为y轴上一点,且始终保持PM+PN最短,当t为何值时,△COM≌△AOB,并求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com